三次多项式


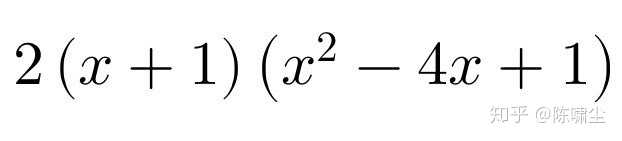
三次多项式是数学领域中的一种常见表达式，由一个未知数三次幂及其前的一次、二次和常数项构成。三次多项式具有其独特的应用价值和几何特征，如二次插值和图形表示等。下面，我们就来探讨一下三次多项式的概念、性质及其应用。


一、三次多项式的概念

三次多项式通常被定义为 f(x) = ax^3 + bx^2 + cx + d 的形式，其中 a、b、c 和 d 是实数系数。这些系数对多项式的形态有着重要的影响，可以通过不同的取值，形成不同形状的曲线或图形。

二、三次多项式的性质


极值点：对于某些三次多项式，它们可能存在极值点，这些点是函数图像的顶点或拐点。极值点的存在使得我们可以通过研究这些点的位置和数量来分析函数的形态。
拐点：在数学上，拐点是曲线或函数图像的弯曲方向发生改变的点。对于三次多项式，如果存在拐点，则说明函数图像在这一点发生了变化。
奇偶性：三次多项式可能具有奇偶性，即 f(-x) = f(x) 或 f(-x) = -f(x)。这有助于我们更好地理解函数的性质和对称性。

三、三次多项式的应用


二次插值：在数据分析和插值过程中，我们可以使用三次多项式来近似或插值未知数据点。这种方法在许多领域都有广泛的应用，如物理、化学和工程等。
图形表示：三次多项式可以用于表示各种形状的曲线和图形，如抛物线、椭圆等。这使得我们可以通过调整系数来生成各种复杂的图形和图像。
数学建模：在数学建模过程中，我们可以使用三次多项式来描述一些复杂的物理现象或系统。例如，在流体力学中，可以使用三次多项式来描述流体在特定条件下的运动轨迹和速度分布等。

总之，三次多项式是一种重要的数学表达式，具有广泛的应用价值和几何特征。通过对其概念、性质和应用的深入理解，我们可以更好地掌握其应用技巧和方法，为实际问题的解决提供有力的数学支持。