一、文章标题


排列组合算法


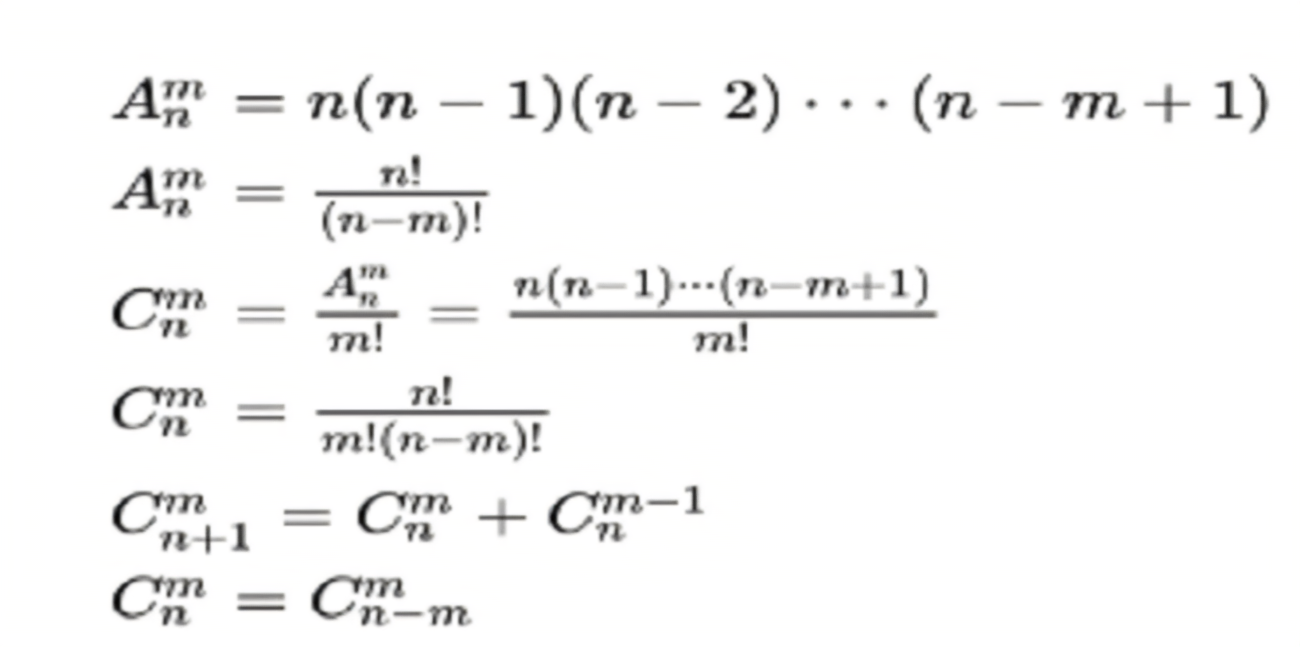
二、文章内容

排列组合算法是计算机科学和数学中常见的基础算法之一，它们被广泛应用于数据处理的多个领域，包括搜索引擎的排序算法、社交网络的图分析、人工智能算法的构建等等。本文将详细介绍常见的几种排列组合算法，帮助您了解它们的原理和特点。

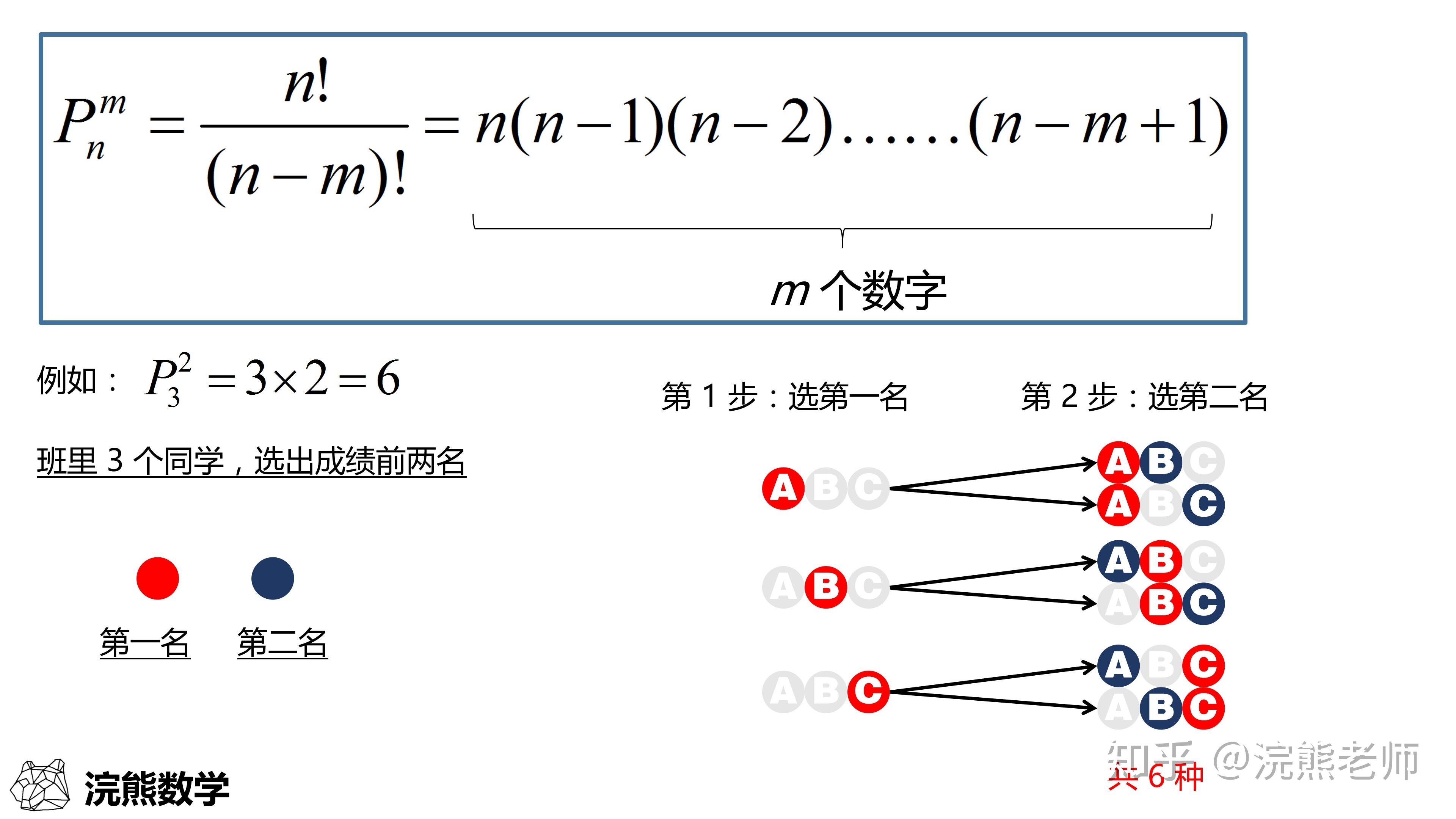
一、简单排列组合算法

最基础且最常见的排列组合算法莫过于“简单排列”和“简单组合”。所谓“简单排列”指的是所有元素可以以任何顺序出现一次，如手写中的单词的字母排序或打印文本中的文本排列等。而“简单组合”则是指从一组元素中选取若干个元素，不考虑顺序，如一个列表中选出所有的子集。

二、全排列算法

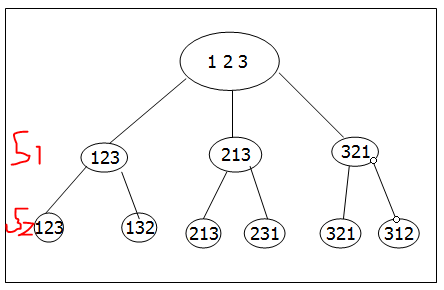
全排列算法是一种用于生成一个集合中所有可能排列的算法。例如，对数组[1, 2, 3]的全排列将得到以下6种不同的序列：[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]。在生成全排列的过程中，可以通过交换相邻元素的顺序，再逐步交换所有其他元素的顺序来实现。

三、递归算法在排列组合中的应用

递归算法在排列组合中扮演着重要的角色。例如，在全排列中，我们可以将第一个元素作为基准，然后对剩余的元素进行全排列，并将这些结果与第一个元素进行组合，从而得到整个集合的全排列。这种递归的思想可以应用于许多其他复杂的排列组合问题中。

四、优化算法：回溯法

回溯法是一种用于解决约束满足问题的算法，也常用于优化排列组合问题。在解决全排列问题时，如果遇到不满足条件的情况，我们可以回溯到上一步重新选择其他元素进行尝试。通过不断回溯和尝试，最终可以找到所有满足条件的排列组合结果。

五、总结

以上就是常见的几种排列组合算法的介绍。这些算法在计算机科学和数学中有着广泛的应用，如搜索引擎的排序算法、社交网络的图分析等。掌握这些算法的原理和特点，可以帮助我们更好地理解和应用它们，从而更好地解决实际问题。同时，随着人工智能和大数据的不断发展，排列组合算法也将有更广泛的应用前景。