一、微分的定义


微分，在数学领域是一个基础但非常重要的概念，主要应用在解决复杂的物理、工程以及各种复杂数据变化等问题的分析和预测上。今天我们将探讨一下微分的定义以及它在日常生活和学术领域中的重要作用。

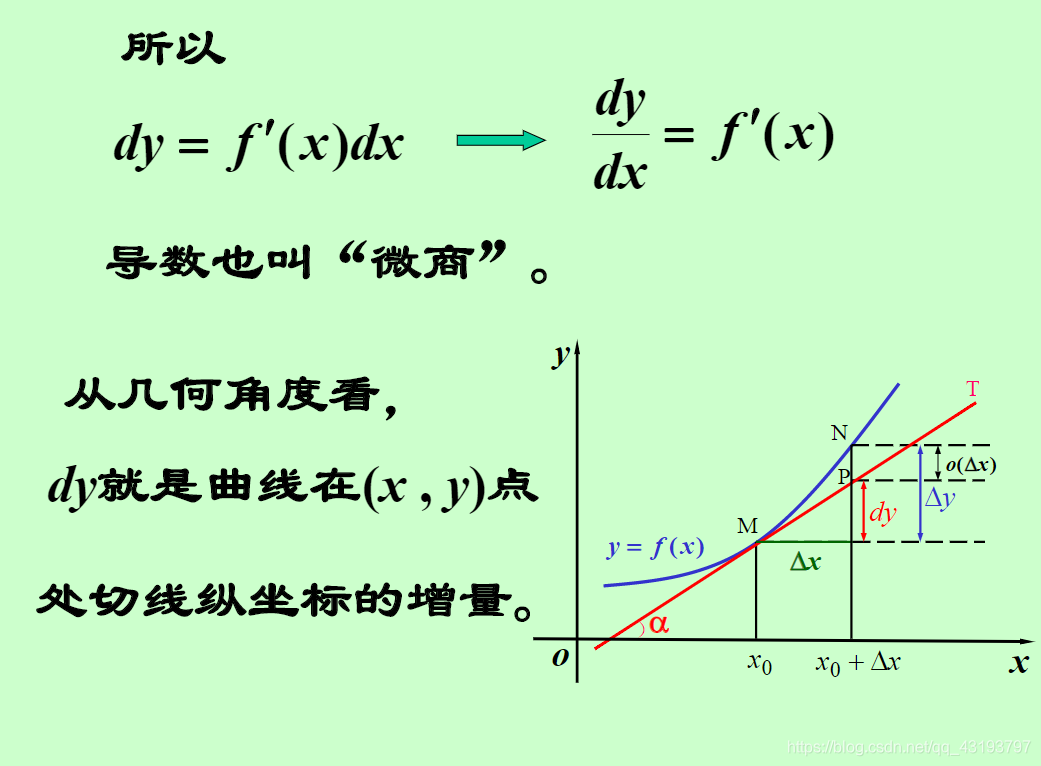
二、微分的起源

微分最初由莱布尼茨和牛顿等人引入并发展起来，是一种计算数学中变化率的工具。通过极限的数学方法，我们可以把复杂的函数关系简化成可计算的变化率。在解决现实生活中的问题时，如物体的速度、路程的变动等，都需要利用到微分。

三、微分的定义

微分在数学上的定义可以简单理解为：函数在某一点的变化率。更具体地说，当函数中自变量有细微的变化时，函数值会如何变化，这就是微分所研究的对象。在数学符号上，我们用f'(x)来表示函数f(x)在x处的导数，也就是f(x)的微分。

四、微分的应用

微分在日常生活和学术领域有着广泛的应用。例如，在物理学中，我们可以通过微分来计算物体的速度和加速度；在经济学中，我们可以通过微分来分析价格的变动和供需关系；在工程学中，我们可以通过微分来分析结构或机械部件的应力变化等。

五、如何学习微分

学习微分首先要理解其基本概念和定义，然后逐步深入学习相关的数学理论和方法。此外，通过大量的练习和实践也是必不可少的。同时，也要学会把学到的知识应用到实际的问题中去，这样可以帮助我们更好地理解和掌握微分的本质和内涵。

总之，微分作为数学中的一个基础且重要的概念，不仅在学术领域有着广泛的应用，也在我们的日常生活中发挥着重要的作用。希望这篇文章能帮助大家更好地理解微分的定义和应用。