一、文章标题：什么是向量


二、文章内容：


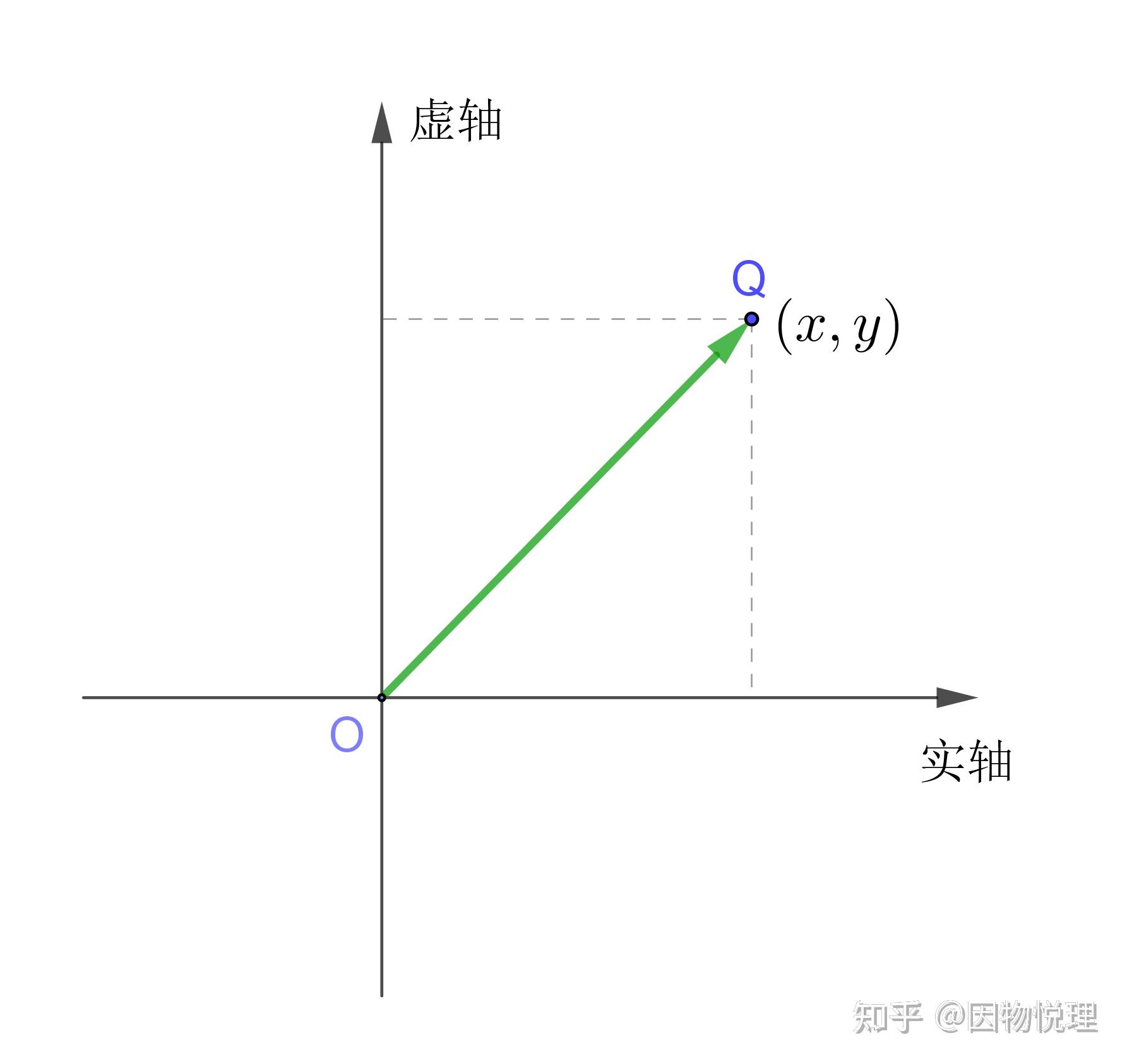
向量，作为数学领域中的一个重要概念，是我们在学习线性代数、物理和工程学时经常遇到的一个名词。那么，究竟什么是向量呢？

1. 向量的定义

向量，简单来说，是一个有大小和方向的量。在数学上，我们通常用带箭头的线段来表示向量，箭头的方向代表向量的方向，线段的长度代表向量的“大小”或“模”。在二维平面上，我们可以将向量看作是两个正交方向（如x轴和y轴）上的投影的组合。

2. 向量的表示

在数学中，我们可以用坐标的形式来表示向量。例如，二维向量可以表示为（x, y）的形式，其中x和y分别代表向量在x轴和y轴上的分量。在三维空间中，我们还可以引入z轴的坐标来描述一个三维向量。此外，我们还可以用点积、叉积等运算来描述向量之间的运算关系。

3. 向量的应用

向量在物理、工程和计算机科学等领域都有广泛的应用。在物理学中，力、速度、加速度等都可以被看作是向量。在工程学中，我们可以用向量来描述物体的运动轨迹、方向等。在计算机科学中，向量也被广泛应用于图像处理、机器学习等领域。

4. 向量的性质

向量具有一些基本的性质。例如，向量具有大小和方向，且大小和方向都可能影响向量的运算结果。此外，向量还具有线性组合、正交等性质。这些性质使得我们可以方便地对向量进行各种运算和操作。

5. 总结

总的来说，向量是一个重要的数学概念，它具有大小和方向两个属性。通过向量的学习和应用，我们可以更好地理解和分析各种物理现象和工程问题。同时，向量的运算和性质也为计算机科学等领域提供了重要的工具和方法。因此，掌握向量的概念和应用对于我们学习和工作都具有重要的意义。