文章标题：真数的取值范围


一、引言


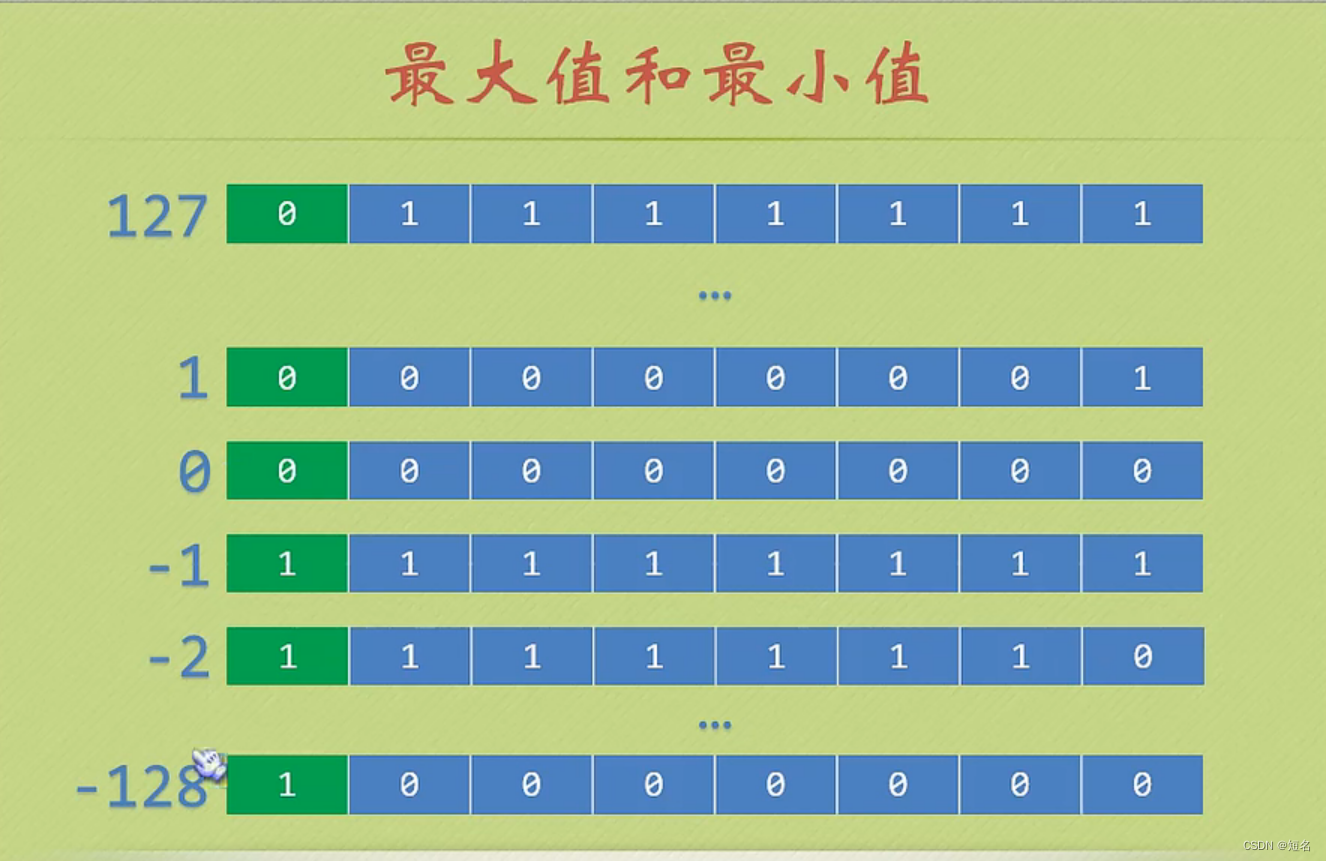
在数学中，真数（Argument）是指函数中对数或幂运算中的基数（在非底数为1的条件下），以及在圆弧等公式中的某些变量。为了深入理解这些函数及相关的计算过程，了解真数的取值范围是十分重要的。本文将探讨真数的取值范围，以及相关的数学背景和运用场景。

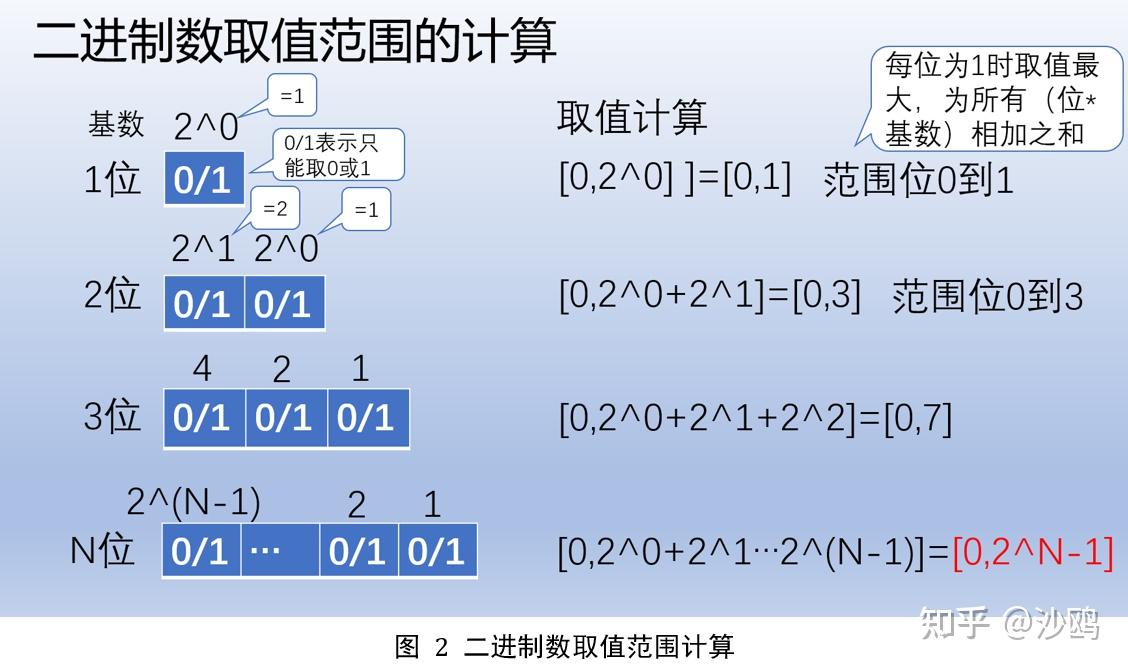
二、真数的定义与基本性质

真数，主要指在函数中对数和幂运算中的变量，它的定义和取值范围会因具体的函数而异。在实数范围内，真数通常指的是大于零的实数。在对数函数中，真数必须为正数，因为对数函数无法处理负数或零的输入值。

三、真数的取值范围

真数的取值范围主要取决于其所在的函数类型。在基本的对数函数中，真数必须大于零且不能等于零。这是因为在实数范围内，没有正的对数对应于零的输入值。此外，不同的对数函数如自然对数（以e为底）或以其他正数为底的对数可能有额外的要求。但基本来说，除了实数值零之外，都是可以被用来作为真数的值域的。

在圆弧和其他特殊公式中，真数的范围取决于特定条件，因此需要我们针对特定情境具体分析。但是大部分情况下，他们都被定义为大于或等于某个特定的值或存在某种约束条件。

四、真数的应用场景

真数的取值范围不仅影响函数的计算过程，还直接关系到我们如何应用这些函数来处理实际问题。例如，在物理学中，我们需要计算某种辐射的强度或者处理指数增长的情况时，就会用到对数和幂运算。这些运算的准确执行都需要我们对真数的取值范围有清晰的了解。

五、结论

理解真数的取值范围对于掌握对数、幂运算和其他涉及到的数学公式至关重要。这不仅有助于我们更好地理解这些公式的定义和性质，也帮助我们在实际应用中正确使用这些公式。希望本文能让你对真数的取值范围有更深入的理解和认识。

以上就是关于真数的取值范围的全部内容，希望能对您有所帮助！