一、卷积符号的介绍与使用


引言


在数学和工程领域，卷积是一个重要的概念，尤其在信号处理、图像处理和深度学习中有着广泛的应用。卷积操作中，我们常常会用到卷积符号，本文将详细介绍卷积符号的由来、使用及在各种场合下的表现形式。

一、卷积符号的起源

卷积的概念最早源于信号处理和统计学。它实际上是一种特殊的加权求和运算，其基本思想是将一个函数（称为冲击响应函数）与另一个函数（称为输入信号）进行“滑动加权”的操作。这个“滑动加权”的过程就是卷积。而这个过程的数学表示就是通过卷积符号来实现的。

二、卷积符号的表示

在数学中，我们通常用星号“”来表示卷积操作。例如，对于两个函数f(x)和g(x)，它们的卷积可以表示为f(x)g(x)。在离散情况下，卷积可以通过一个特定的公式来计算；而在连续情况下，卷积则表示为一种积分运算。

三、卷积符号在各个领域的应用


信号处理：在信号处理中，卷积常常用于滤波、降噪等操作。通过将信号与一个冲击响应函数进行卷积，可以实现对信号的特定处理。
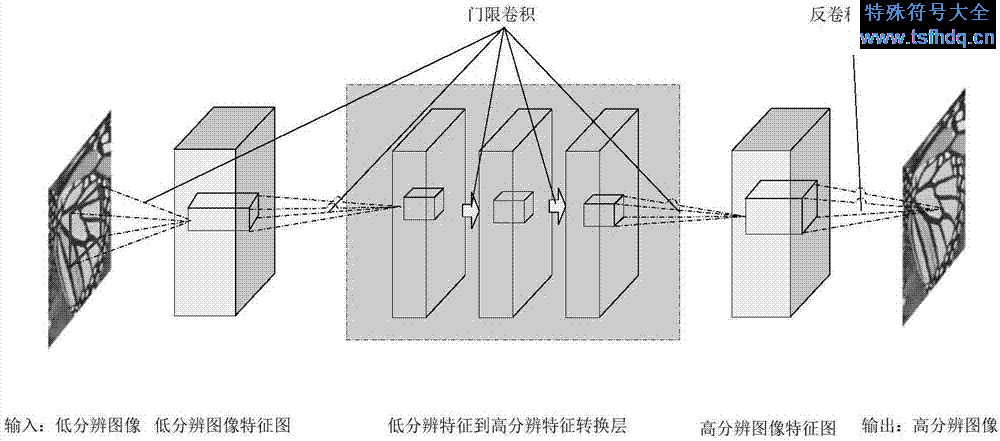
图像处理：在图像处理中，卷积被广泛应用于图像的边缘检测、特征提取等操作。通过不同的冲击响应函数（即卷积核），可以实现不同的图像处理效果。
深度学习：在深度学习中，卷积神经网络（CNN）是最重要的模型之一。其中，卷积操作被大量用于特征提取和分类等任务中。

四、结论

卷积符号作为数学表达的重要工具，在信号处理、图像处理和深度学习等领域都有着广泛的应用。通过对函数的加权求和运算，我们可以实现信号的滤波、降噪以及图像的特征提取等任务。而卷积神经网络更是将这一概念推向了新的高度，成为了现代人工智能的重要基石之一。

本文详细介绍了卷积符号的起源、表示及其在各个领域的应用，希望能对大家对卷积这一概念有更深入的理解。如需进一步学习卷积符号的使用以及在各领域中的应用案例，可以参考相关的专业书籍和论文进行学习。