文章标题：递归与迭代


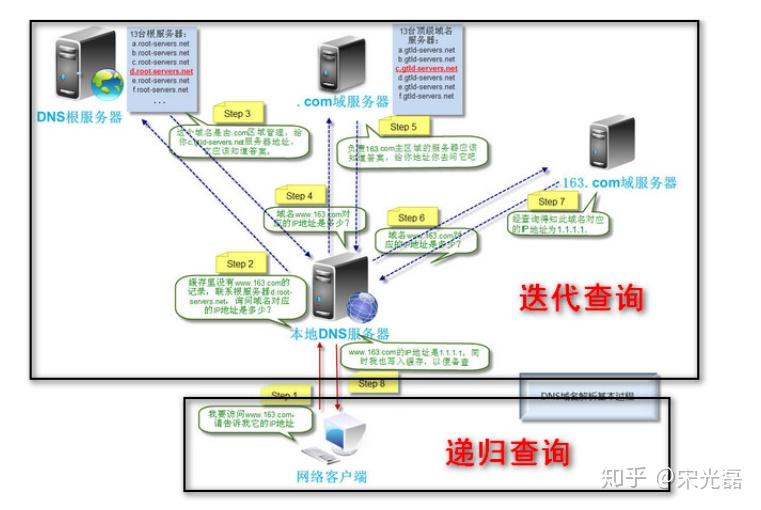
一、递归与迭代简介


在计算机科学中，递归和迭代是两种常见的算法处理方式。它们各自有着独特的优势和适用场景。


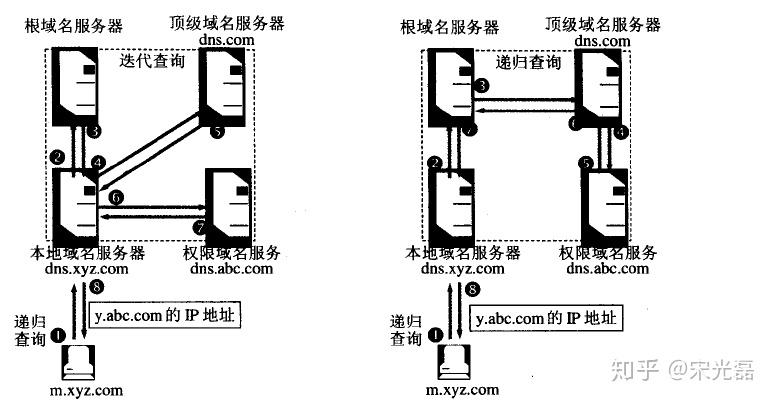
递归

递归是一种自我调用的算法设计方法。在处理问题时，递归算法将问题分解为更小、更简单的子问题，并将这些子问题的解决方案组合起来以解决原始问题。这个过程一直重复进行，直到达到一个基础条件或称为“终止条件”。递归常见于树的遍历、分形图的绘制等问题。


迭代

迭代则是通过反复应用某种算法规则来逐步解决问题的方法。它不是通过减少问题规模来解决整个问题的，而是每次迭代都会缩小问题的一部分或获得更多关于问题的信息。迭代的优点在于可以通过连续的步骤逼近解的近似值，对于寻找近似解或迭代至解收敛的场景非常有效。

二、递归与迭代的比较

虽然递归和迭代都可以解决某些问题，但它们各有特点和适用场合。一般来说，当问题的结构有明显的递归特性时，递归更容易理解。而在求解某类数值问题时，尤其是对效率要求较高的情况下，迭代可能是更好的选择。此外，在处理一些特殊问题时，如深度搜索或树形结构等，递归可以发挥其优势。

三、实际应用中的例子


递归应用：排序算法中的归并排序和快速排序都是通过递归实现的。在归并排序中，将一个大数组分割为两个小数组，分别对它们进行排序，然后将两个有序的小数组合并成一个有序的大数组。这个过程会一直递归进行，直到子数组的规模足够小可以直接排序为止。
迭代应用：求解平方根和方程近似解的问题常常使用迭代方法。例如，牛顿迭代法就是通过不断迭代来逼近一个数的平方根或某个方程的解。

四、总结

总的来说，递归和迭代都是解决算法问题的有效方法。它们各自有着独特的优点和适用场景。在编写程序时，选择哪种方法取决于问题的具体性质和所需的时间、空间复杂度等因素。无论选择哪种方法，都应遵循程序设计的最佳实践原则，以确保代码的可读性、可维护性和性能优化。