方向向量是什么
一、概念简述


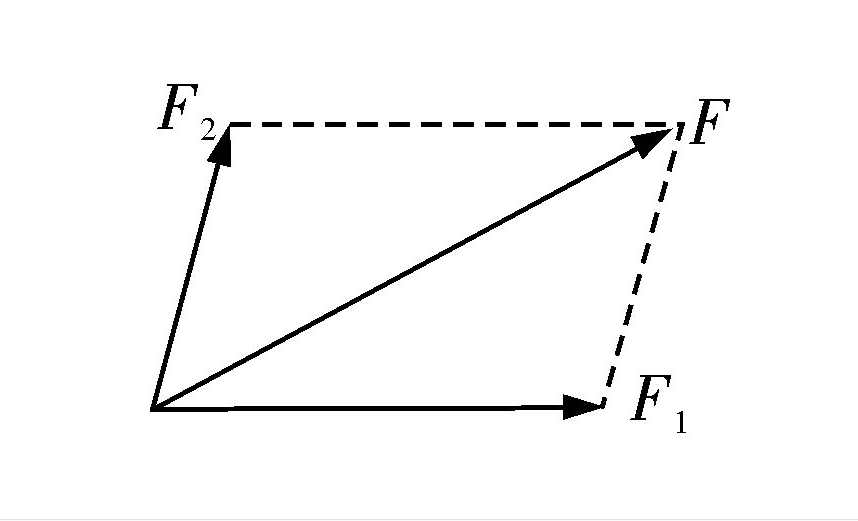
方向向量是描述或定义在空间或平面中某一方向的工具，常用于数学、物理和工程等多个领域。在几何学中，方向向量是一个具有方向和大小的矢量，用于表示一个特定的方向。在物理学中，方向向量常用于描述速度、力等物理量的方向。


二、基本特性



方向性：方向向量明确地指明了方向，它代表了从一个点延伸到另一个点的路线。这个方向可以用一组数来表示，比如x轴、y轴和z轴的三个分量的数值，反映了它在空间中的三维指向。



大小：除了方向外，方向向量还有大小的概念。在空间中，大小代表了其长度的数值。因此，方向向量可以同时传达物体在空间中的方向和规模。



变化性：对于固定的空间参考点而言，如果方向和长度（大小）中的任何一部分发生了变化，那么它的方向向量就会发生改变。比如当我们需要计算一条不同角度的直线的方向向量时，即使长度保持不变，仅仅因为角度的变化，方向向量就会发生相应的改变。



三、应用场景



数学和几何学：在解析几何和向量代数中，方向向量被广泛用于计算平面的倾斜度、求解曲线或直线的法线等操作。



物理学：在力学中，速度、加速度等矢量均可以表示为方向向量，有助于分析和计算物理过程的变化和路径。在光学中，波动的传播也经常用方向向量来描述。



工程学：在工程学中，如机械设计、建筑设计和计算机图形学等领域，方向向量被用来表示物体的位移、速度等动态特征以及定向建模等工作。



四、如何创建与计算

一般来说，计算或确定一个点的方向向量涉及到基于两点之间相对位置的关系进行计算。在二维空间中，我们可以通过确定一个点相对于另一个点的x轴和y轴的坐标差来计算其方向向量；在三维空间中，我们则需要加上z轴的坐标差进行计算。另外，通过矢量分析或数学公式也能进行更为复杂的计算。

总之，方向向量是一个非常实用的数学工具，它在许多领域都有着广泛的应用。通过了解其基本概念和特性以及应用场景和计算方法，我们可以更好地理解和应用它。