一、文章标题


整数集合


二、文章内容

整数集合是数学中一个基本且重要的概念，它涵盖了正整数、负整数以及零的集合。这个集合在数学领域中有着广泛的应用，包括但不限于代数、数论、集合论等。

一、整数的定义

整数是指包括正整数、负整数和零的数集。它没有小数或分数的形式，是一个由一系列独立的、不可再分的数值构成的集合。

二、正整数的概念及性质

正整数是大于零的整数，它具有明确的大小关系，可以用来进行大小比较。正整数集合具有无序性，也就是说，其内部元素之间没有固定的顺序关系。此外，正整数的集合是可数的，可以按照一定的顺序一一列举出来。

三、负整数的概念及性质

负整数是小于零的整数，它在数轴上位于原点的左侧。负整数与正整数具有相反的数学性质，如大小关系等。负整数的集合同样具有无序性和可数性。

四、整数集合的应用


代数：在代数中，整数集合是基础元素之一，用于构建更复杂的数学结构，如多项式、方程等。
数论：在数论中，整数集合是一个重要的研究对象，包括对整数的性质、规律和结构的探讨。如质数、合数、素数分布等问题的研究都离不开整数集合。
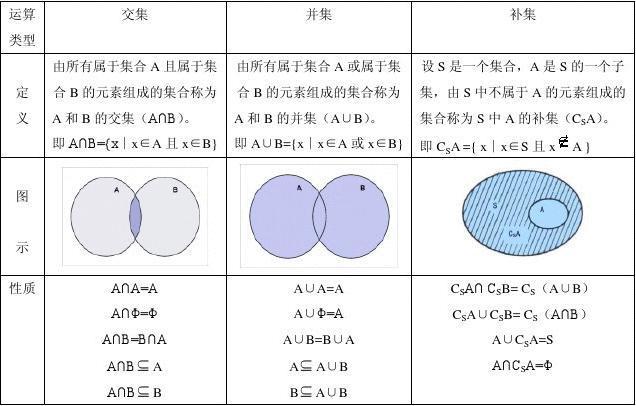
集合论：在集合论中，整数集合是基本的数集之一，用于构建更复杂的数学结构，如数集的运算等。

此外，在日常生活中，整数集合也扮演着重要的角色。如我们在购物时经常使用整数的货币单位，又如计算机中使用的二进制码本质上是基于整数的表示方式等。

总之，整数集合作为数学中的一个基本概念，具有广泛的应用和重要的意义。我们应该深入了解并掌握它的基本性质和特点，为进一步学习数学打下坚实的基础。