补集的定义
一、概念简介
在数学领域中，补集是某一集合论中一个重要的概念。简单来说，补集就是一个集合中所有不属于另一个特定集合的元素所组成的集合。在讨论补集时，我们通常需要先确定一个全集，即所有可能元素的集合。补集则是在这个全集的范围内，不属于另一个给定集合的所有元素组成的集合。


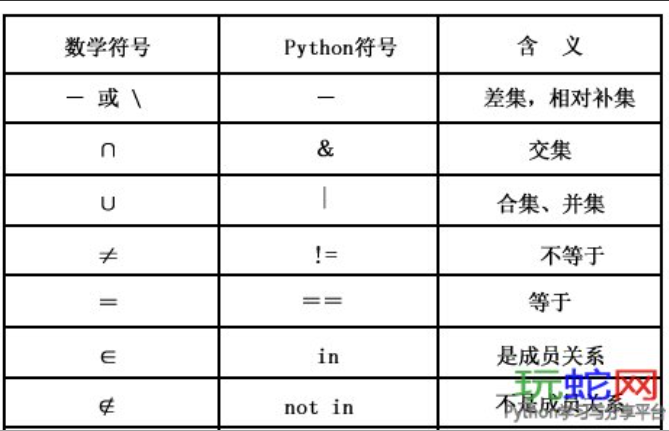
二、补集的数学定义
假设我们有两个集合A和B，全集为U，那么集合A相对于全集U的补集A'，即U中所有不属于A的元素组成的集合。同样地，对于集合B，其相对于全集U的补集B'也是U中所有不属于B的元素组成的集合。


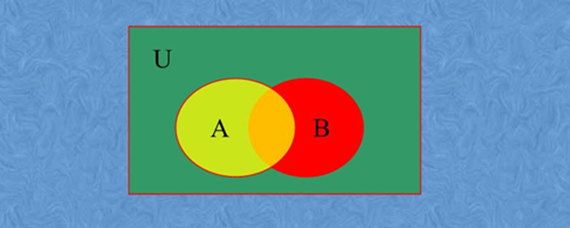
三、补集的性质

补集是相对于全集而言的，没有全集的概念，就无法定义补集。
任何一个集合与其补集的并集等于全集，即A∪A' = U。
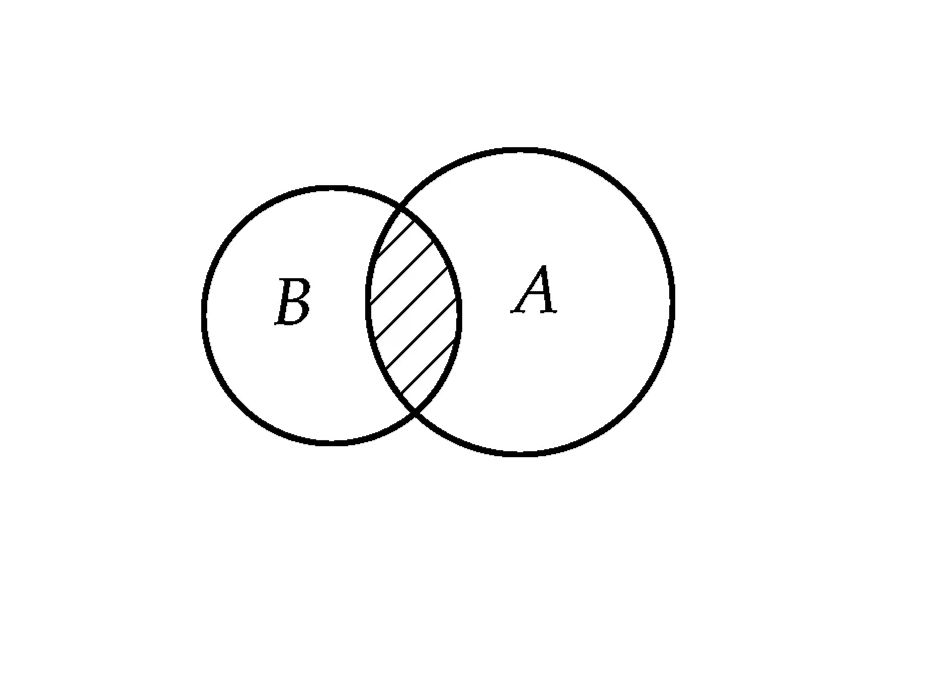
任何一个集合与其补集的交集为空集，即A∩A' = ∅。

四、补集的应用
补集在数学中有着广泛的应用，如逻辑运算、集合运算等。在计算机科学中，补集的概念也被广泛应用在数据结构、算法设计等领域。同时，在现实生活中，补集的概念也有着广泛的应用，如在市场分析、统计学等领域。

五、总结
补集是数学中一个重要的概念，它描述了一个集合中所有不属于另一个特定集合的元素所组成的集合。通过补集的概念，我们可以更好地理解集合之间的关系和运算。同时，补集在各个领域都有着广泛的应用，是数学和其它学科之间的一座重要桥梁。了解并掌握补集的概念和性质，对于提高我们的数学素养和解决实际问题都有着重大的意义。