三次项
主机域名文章
2025-01-22 19:25
1024
三次项

在数学领域,三次项是一个重要的概念,特别是在代数和微积分中。三次项指的是一个多项式中,未知数的三次方乘以一个系数。例如,在多项式ax^3 + bx^2 + cx + d中,ax^3就是三次项。下面,我们将更详细地探讨三次项及其相关概念。

一、三次项的基本定义
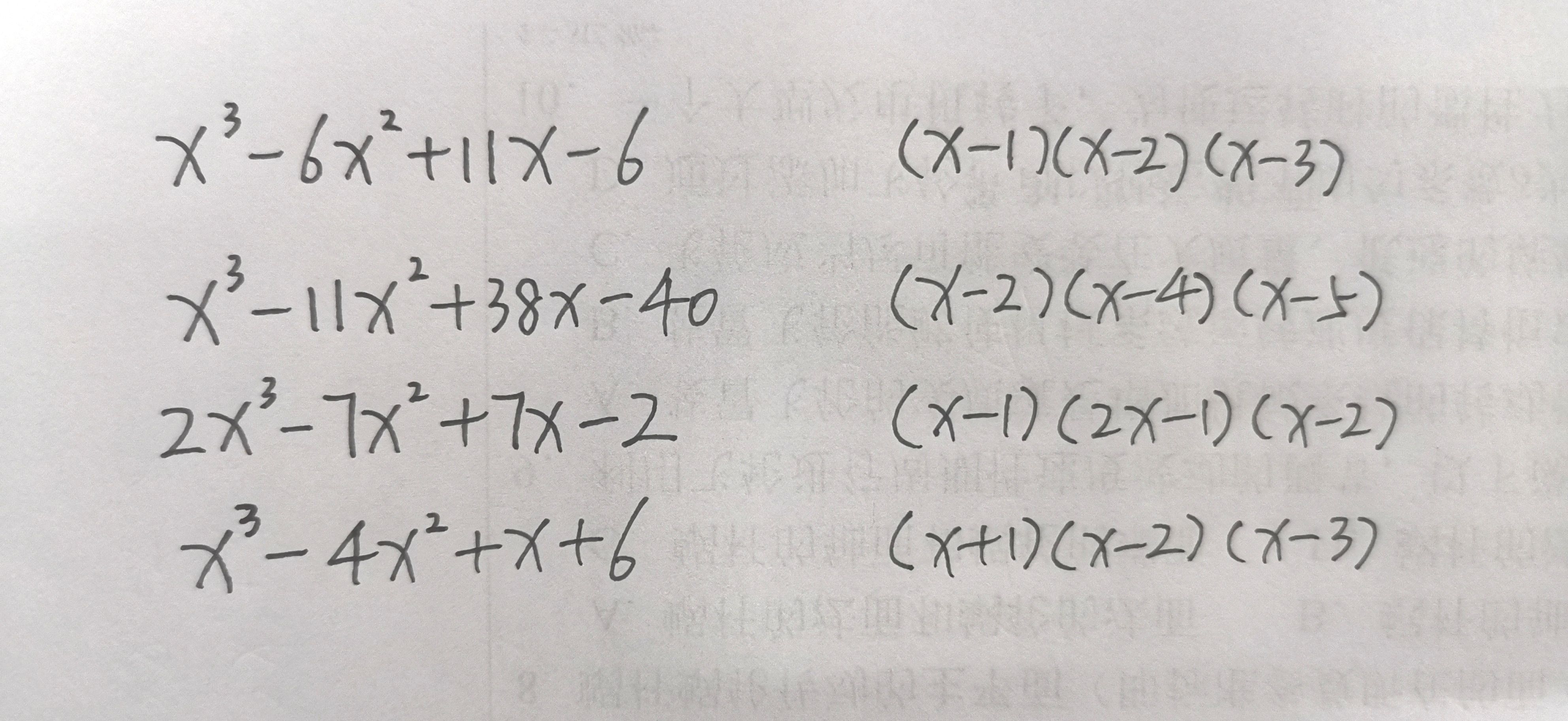
三次项是由三个变量(通常为x)相乘得到的项。在代数表达式中,它表示了未知数的三次方。在多项式中,每个变量(如x)的指数都代表其幂次,而三次项的指数恰好为3。
二、三次项在数学中的应用
- 多项式运算:在多项式相加或相减的过程中,三次项是影响多项式结果的重要因素之一。
- 微积分:在微积分中,三次项经常出现在各种函数中,如多项式函数、三角函数等。这些函数在研究物理现象、工程问题等方面有着广泛的应用。
- 代数方程:在解代数方程时,三次项常常是方程解的关键因素。例如,解三次方程时,需要找出使三次项和其他项相等的x值。
三、三次项的特殊形式
- 高阶三次项:当多项式中的三次项系数较大时,它可能对多项式的整体形状产生重要影响。例如,一个高阶三次项可能导致多项式图像向上或向下弯曲。
- 低阶三次项:在某些情况下,即使三次项的系数较小,它仍然可能对多项式的性质产生重要影响。这通常发生在其他低阶项(如一次项或二次项)的系数较小或为零时。
四、结论
综上所述,三次项是数学领域中的一个重要概念。无论是在代数运算、微积分、还是在其他数学分支中,它都发挥着至关重要的作用。通过对三次项的研究和理解,我们可以更好地掌握数学中的多项式、函数等基本概念,从而更好地解决各种数学问题。
以上内容只是对三次项的基本介绍和解释,如需更深入的研究和学习,建议查阅相关数学教材或文献。
Label:
- 关键词:三次项
- 多项式
- 微积分
- 代数方程
- 高阶三次项
- 低阶三次项

