标题：复数绝对值详解
当我们探讨复数的性质和操作时，一个重要的概念就是复数的绝对值。复数是一种扩展了实数域的数学概念，它不仅包含了实数，还包含了带有虚部的数。下面我们将详细探讨复数绝对值的定义、性质和计算方法。


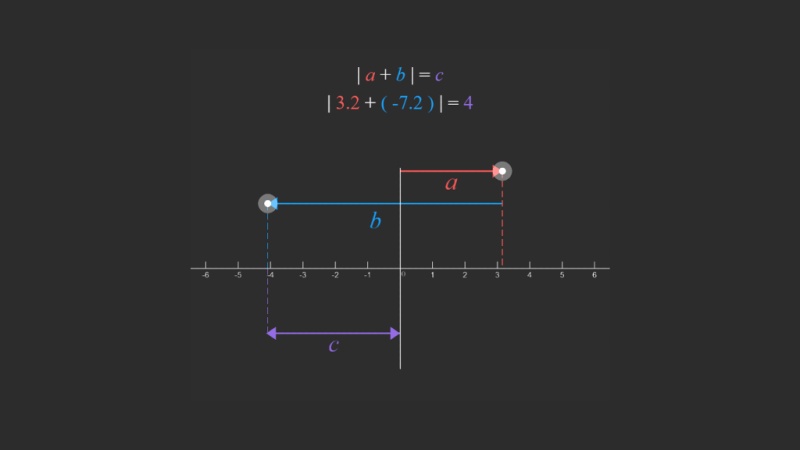
一、复数绝对值的定义
复数的绝对值，也称为模（Modulus），是一个非常重要的概念。对于任意复数z，其形式为z=a+bi（a和b都是实数），其绝对值定义为：


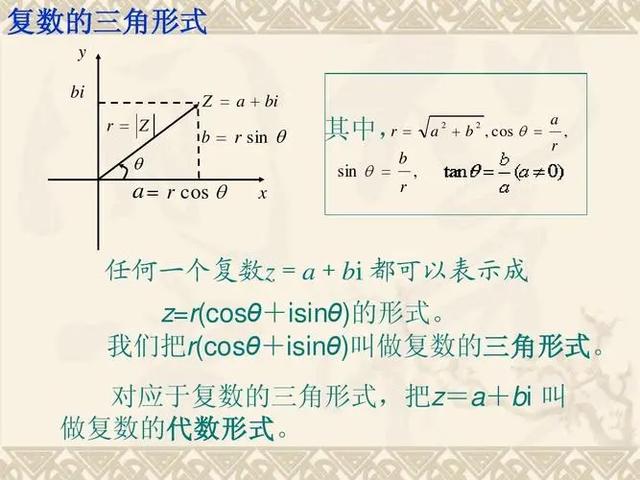
|z| = √(a^2 + b^2)

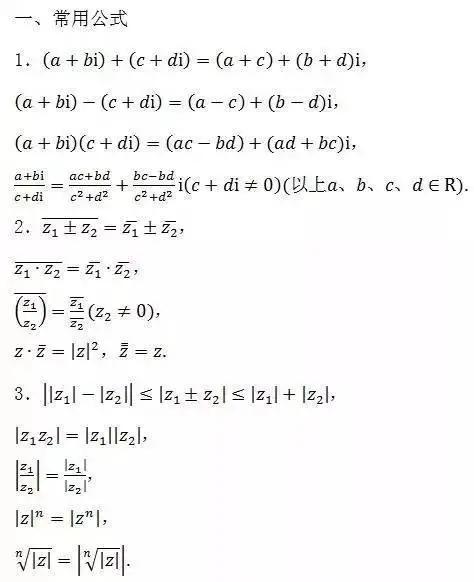
这个定义表明，复数的绝对值是其实部和虚部平方和的平方根。当虚部b=0时，复数就变成了实数，其绝对值就是实数本身。

二、复数绝对值的性质

非负性：对于任意复数z，其绝对值总是非负的，即|z|≥0。
三角不等式：对于任意两个复数z1和z2，都有|z1+z2|≤|z1|+|z2|。这是三角不等式的直接应用。
模的运算性质：复数的模满足一些基本的运算规则，如模的乘法、除法等。

三、复数绝对值的计算方法
计算复数的绝对值非常简单，只需要按照上述公式进行计算即可。例如，对于复数z=3+4i，其绝对值为：

|z| = √(3^2 + 4^2) = √(9 + 16) = √25 = 5

四、复数绝对值的应用
复数的绝对值在数学、物理和工程等多个领域都有广泛的应用。例如，在电路分析中，复数可以用来表示交流电的电压和电流，而复数的绝对值则可以表示电压或电流的幅度。在信号处理、控制论等领域，复数的绝对值也常常被用来描述信号的强度或系统的稳定性等。

总结
以上就是关于复数绝对值的详细介绍。通过了解复数绝对值的定义、性质和计算方法，我们可以更好地理解复数的性质和运算规则，同时也能更好地应用复数在各个领域中的实际意义。