对数的导数公式


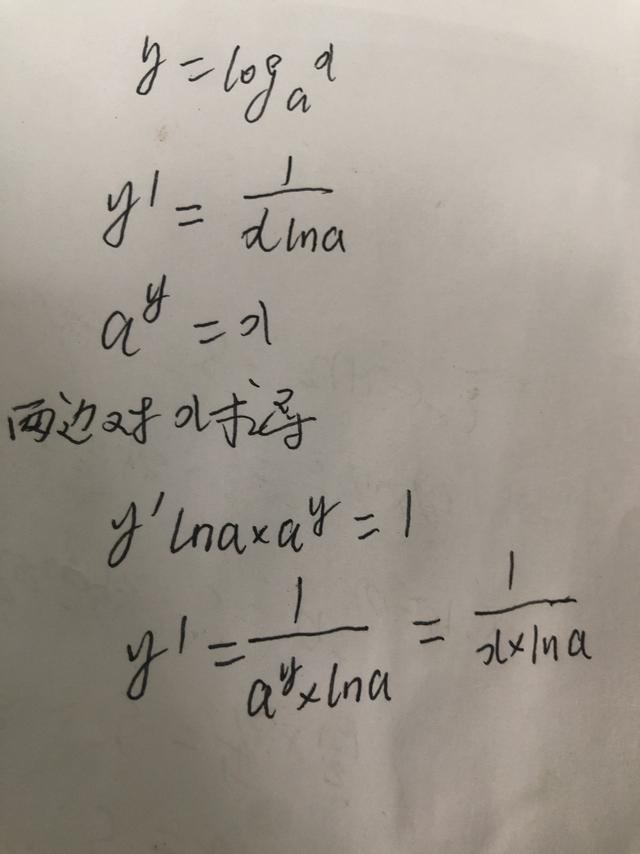
当我们涉及到高等数学的学习和探索时，常常会遇到导数的概念，以及基于该概念的复杂函数的导数问题。这其中，对数的导数公式也是需要掌握的一个重要知识点。


首先，我们要明确对数的基本概念。对数，作为数学中的一种运算方式，在多个领域都有着广泛的应用。其具体表现为，当x的对数形式为y = loga(x)时，即y表示以a为底x的对数。

那么，对于这种形式的对数函数，其导数公式是什么呢？

根据高等数学的导数理论，我们可以得出：(log_a(x))' = 1 / (x*ln(a))，也就是说，对于底数为a的对数函数，其导数为“以x为原函数、以ln(a)为常数因子”的倒数。

那么这个公式是怎么来的呢？我们可以通过函数的极限性质来推导。此处限于篇幅不再赘述具体的推导过程，而是重点关注该公式的实际应用。

对数的导数公式在求取某些复合函数或复杂函数的导数时非常重要。当与其它微积分知识点相结合时，我们往往可以通过该公式迅速找出某个特定函数的导数。例如，对于函数f(x) = log_a(g(x))，如果g(x)的导数已知，那么可以通过链式法则和上面的对数导数公式求出f(x)的导数。

同时，我们还需要注意的是对数的导数公式的实际意义和应用场景。这些内容需要我们深入学习数学原理并联系实际案例进行理解。因此，对于数学爱好者或专业学习者来说，熟练掌握对数的导数公式是非常重要的。

总之，对数的导数公式是高等数学中一个重要的知识点。了解并熟练掌握该公式的原理、应用方法和实例解析有助于我们在实际问题中迅速求解复杂的导数问题。此外，持续的学习和实践可以帮助我们深入理解该知识点的重要性并学会运用它来解决实际问题。希望本篇文章的阐述能够让你更加清楚地掌握和理解对数的导数公式及其在实践中的应用。