共线性检验


在统计学和数据分析中，共线性检验是一个非常重要的步骤。它主要用于检测两个或多个变量之间是否存在高度相关性，这种相关性可能导致回归模型中系数估计的准确性降低，进而影响模型的预测能力。本文将详细介绍共线性检验的原理、方法和应用场景。


一、共线性检验的原理

共线性是指两个或多个变量之间的相关程度较高，这可能是由于他们同时受到类似的因素影响或者相互影响的结果。在多元回归分析中，当解释变量（自变量）之间存在较强的相关性时，就会产生共线性问题。这种情况下，回归模型的系数估计可能不准确，导致模型的预测能力下降。

二、共线性检验的方法



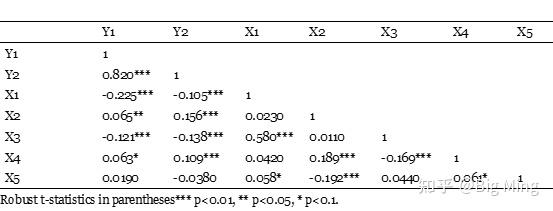
计算相关系数：首先，我们可以通过计算变量之间的相关系数（如皮尔逊相关系数）来初步判断是否存在共线性。如果相关系数接近1或-1，就说明这两个变量之间存在高度的相关性。



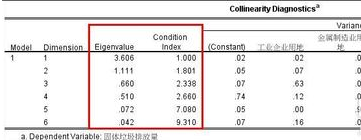
方差膨胀因子（VIF）：VIF是一种常用的共线性检验方法。VIF的计算公式中包含了模型中所有解释变量的相关系数信息，如果VIF值大于某个阈值（如10），就说明可能存在共线性问题。



矩阵对角线法：这是一种比较复杂的方法，涉及到回归模型的系数矩阵的行列式和特征值等。通过观察矩阵对角线上的元素值和矩阵行列式的值来判定是否共线。



三、共线性检验的应用场景

在回归分析、预测模型等场景中，我们常常需要用到共线性检验来检测数据是否适合进行建模。例如，在房价预测模型中，如果影响房价的多个因素之间存在高度相关性，那么就需要进行共线性检验来确保模型的准确性。

总之，共线性检验是数据分析中一个重要的步骤，它可以帮助我们检测数据是否存在共线问题并采取相应的措施来避免或解决这个问题。通过使用合适的方法和工具进行共线性检验，我们可以确保模型的准确性和预测能力。