一、文章标题：什么是伴随矩阵


二、文章内容


在数学领域中，伴随矩阵（Adjugate Matrix）是一个重要的概念，它常常出现在线性代数的学习和研究中。伴随矩阵是矩阵理论中一个非常有用的工具，它不仅在数学学科内部有着广泛的应用，也在其他科学领域如物理、计算机科学等有重要应用。

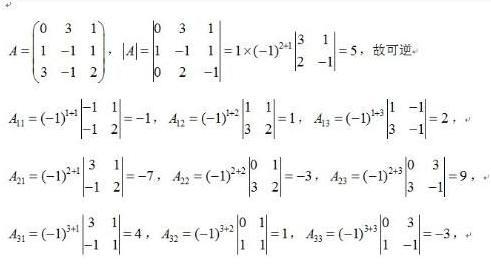
1. 伴随矩阵的定义

对于任何方阵（即行数和列数相等的矩阵），其伴随矩阵是由该矩阵的代数余子式构成的新矩阵，转置后得到的结果即为伴随矩阵。具体来说，一个n阶方阵A的元素ai,j（第i行第j列的元素）的代数余子式是去掉该元素所在的行和列后得到的（n-1）阶方阵的行列式。

2. 伴随矩阵的性质

（1）如果A是可逆矩阵（即存在逆矩阵），那么A的逆矩阵等于A的伴随矩阵除以A的行列式的值。

（2）若一个方阵的某几行的元素均为零或无法定义伴随矩阵时，那么其无伴随矩阵。

（3）当矩阵A是满秩的，那么其伴随矩阵也具有非零的行列式值。

3. 伴随矩阵的应用

（1）在解线性方程组时，如果系数矩阵是方阵且可逆，那么可以通过其伴随矩阵求解未知数向量。

（2）在计算行列式的值时，如果直接计算复杂度较高，可以通过计算其伴随矩阵来简化计算过程。

（3）在解决图论问题时，某些问题可通过关联矩阵（Matrix-Tree 定理中提到的一种特殊的伴随矩阵）来求解。

4. 计算方法

计算一个矩阵的伴随矩阵需要先计算该矩阵的代数余子式。再由代数余子式构成的矩陈就是伴随矩阵了。其中行列式的值决定了其逆的倍数关系。对于计算过程，需要一定的数学基础和耐心。不过一旦掌握了方法，就可以快速地得到结果了。

总的来说，伴随矩阵是线性代数中一个重要的概念，它不仅在数学学科内部有着广泛的应用，也在其他科学领域如物理、计算机科学等有重要应用。掌握其概念、性质和计算方法对提高解题能力具有重要的作用。希望通过以上内容的介绍和学习，能够让您对伴随矩阵有更深入的了解。