文章标题：arccos图像


在数学中，反余弦函数（arccos）是一种非常重要的函数，它与余弦函数（cos）是互为反函数的。它可以帮助我们更深入地理解三角函数的性质和特点，同时也被广泛应用于各种数学和物理问题中。本文将介绍arccos图像的基本概念和特点。


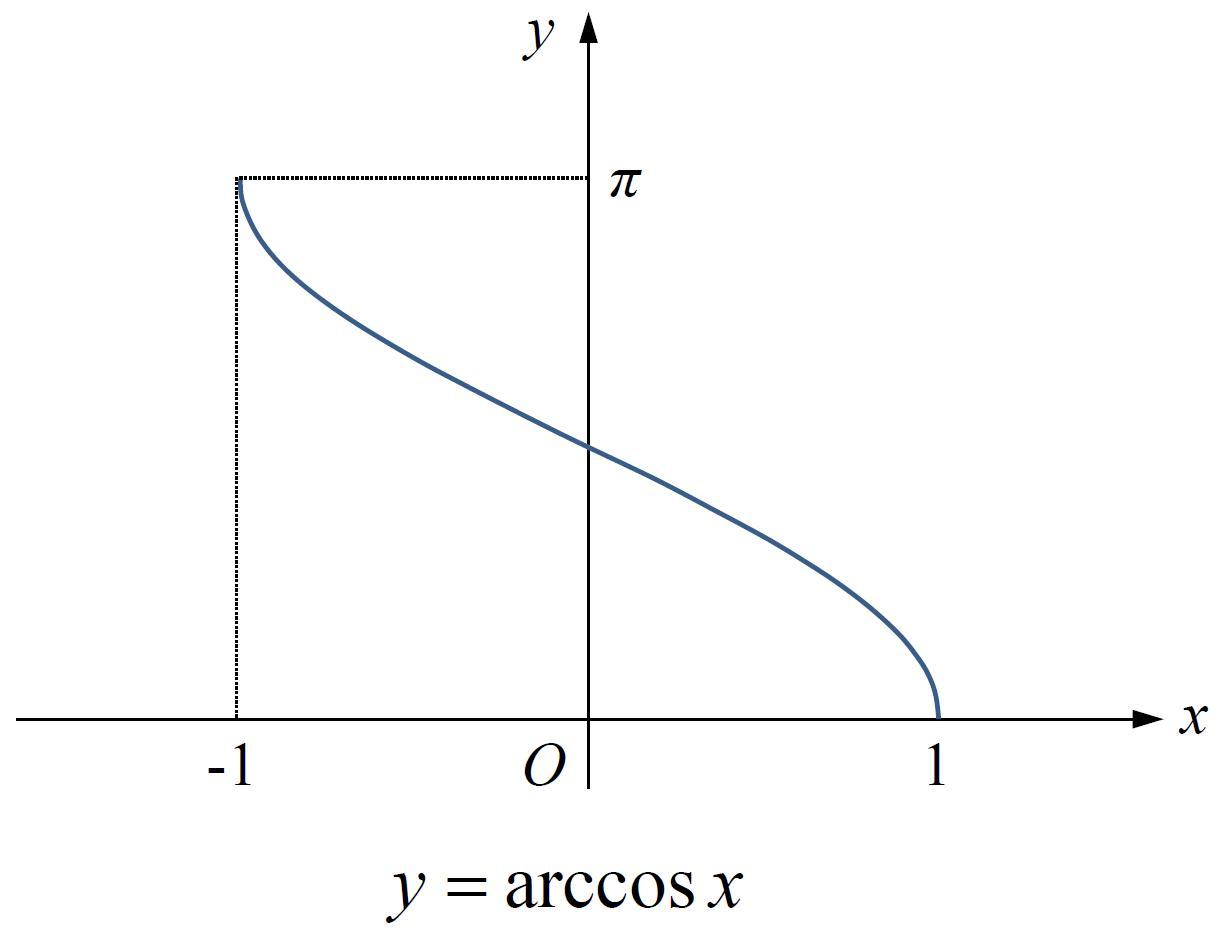
一、arccos函数的定义

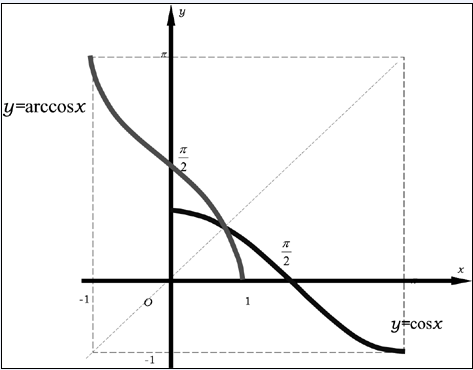
反余弦函数是余弦函数的反函数，其定义域为[-1, 1]，值域为[0, π]。也就是说，给定一个x值在[-1, 1]之间，arccos函数可以求出对应的角度值。这个角度值表示的是，当以x为余弦值时，对应的角度是多少。

二、arccos图像的基本特点

arccos函数的图像是一个以y轴为对称轴的曲线。在定义域[-1, 1]内，它的值随着x的增大而减小，即当x越接近于1时，arccos函数的值越小。而当x从-1到0变化时，arccos函数的值则从π逐渐减小到0。

具体来说，arccos图像的形状类似于一个倒置的半圆弧。在x=0处，其值是π/2；而在x=-1或x=1时，其值则分别接近于0或π。在整个定义域内，它的值与cos值在[0, π/2]和[π/2, π]之间存在一一对应的关系。

三、arccos图像的应用

反余弦函数的应用非常广泛，主要表现在以下几个方面：



在几何学中，arccos函数可以用于计算平面上的角度。例如，当我们需要计算两条线之间的夹角时，可以使用反余弦函数根据已知的cos值求出相应的角度值。



在物理中，arccos函数也有重要的应用。比如通过反余弦函数可以求解某些力学问题中的角度关系等。



在数学中，反余弦函数是三角函数的重要部分之一，对于理解三角函数的性质和特点有重要作用。



综上所述，arccos图像在数学和其他学科领域都有重要的应用价值。了解和掌握它的基本概念和特点有助于我们更好地理解和应用反余弦函数，提高数学和其他学科的学习效果。