互相关函数
主机域名文章
2025-01-07 14:55
369
一、文章标题
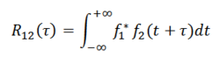
互相关函数
二、文章内容
在信号处理和统计学中,互相关函数是一种非常重要的工具,它用于描述两个信号之间的相似性或相互关系。在许多领域,如音频处理、图像处理、时间序列分析等,互相关函数都有着广泛的应用。
一、互相关函数的定义
互相关函数是一种衡量两个信号之间相似性的函数。在数学上,它可以通过计算两个信号在不同时间点上的乘积和来得到。具体来说,对于两个信号x(t)和y(t),它们的互相关函数Rxy(τ)可以定义为:
Rxy(τ)=∫x(t)y(t+τ)dtRxy(τ) = \int x(t)y(t+\tau)dtRxy(τ)=∫x(t)y(t+τ)dt
其中,τ是时间延迟参数,表示y(t)相对于x(t)的延迟时间。
二、互相关函数的应用
- 音频处理:在音频处理中,互相关函数常被用于语音识别、音频信号的同步和噪声消除等方面。例如,在语音识别中,可以通过计算语音信号与已知的模板信号之间的互相关函数,来识别出语音信号中的关键词或短语。
- 图像处理:在图像处理中,互相关函数可以用于图像配准和图像融合等任务。通过计算两幅图像之间的互相关函数,可以找到它们之间的相似性和差异,从而实现图像的精确配准和融合。
- 时间序列分析:在时间序列分析中,互相关函数可以用于分析时间序列数据之间的相互关系和依赖性。例如,在金融领域中,可以通过计算股票价格时间序列之间的互相关函数,来分析不同股票之间的相互关系和影响。
三、互相关函数的性质
互相关函数具有一些重要的性质。首先,它是对称的,即Rxy(τ)=Ryx(−τ)Rxy(\tau) = Ryx(-\tau)Rxy(τ)=Ryx(−τ)。其次,当τ=0\tau = 0τ=0时,Rxy(0)Rxy(0)Rxy(0)表示两个信号的平均功率或能量。此外,互相关函数还可以用于确定两个信号之间的延迟时间,这在许多应用中都是非常重要的。
四、总结
互相关函数是一种非常重要的工具,它能够描述两个信号之间的相似性或相互关系。在信号处理和统计学中,互相关函数有着广泛的应用,包括音频处理、图像处理、时间序列分析等领域。通过计算互相关函数,我们可以找到两个信号之间的相似性和差异,从而实现各种应用任务。因此,掌握互相关函数的基本概念和应用方法对于从事信号处理和统计学研究的人来说是非常重要的。
Label:
- 关键词: 互相关函数
- 信号处理
- 统计学
- 音频处理
- 图像处理
- 时间序列分析
- 时间延迟参数
- 对称性
- 平均功率
- 能量

