高斯拟合
引言


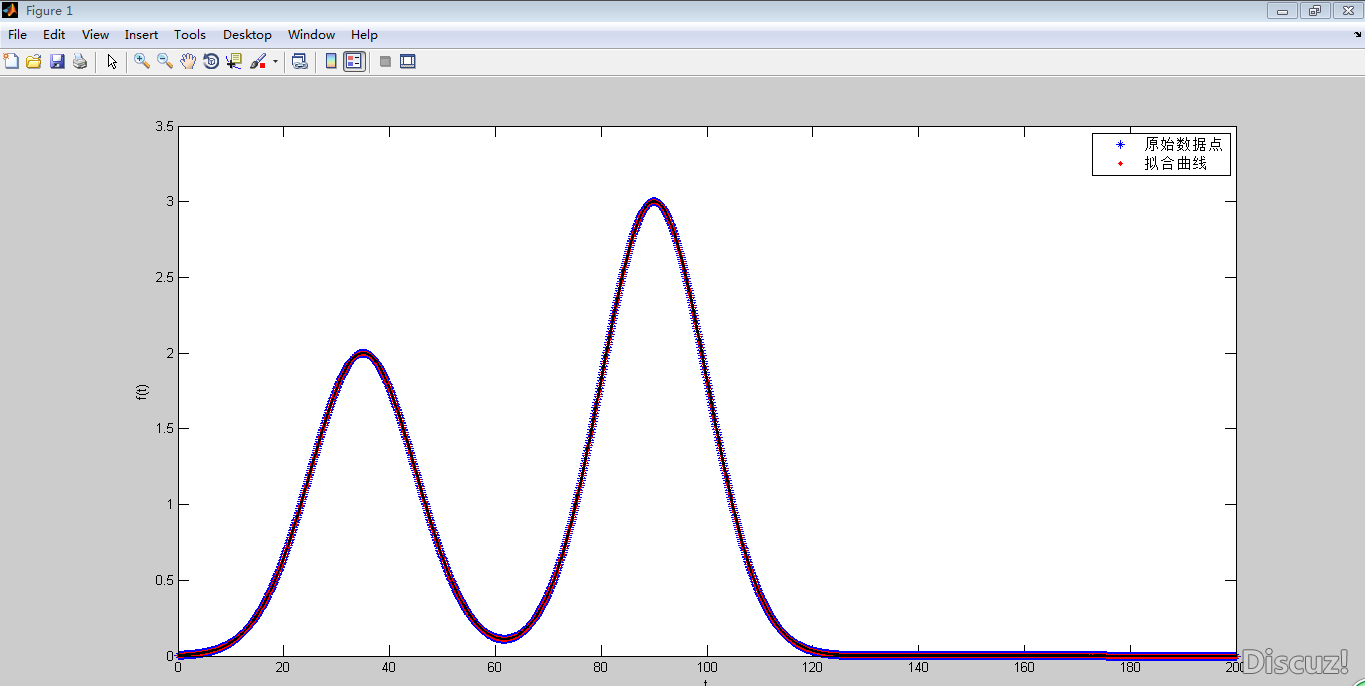
在众多的曲线拟合方法中，高斯拟合作为一种常用于分析、估计以及求解连续变量上的函数的技术，广泛应用于信号处理、统计计算和机器学习等领域。下面我们将从多个角度介绍高斯拟合的基本原理和常见应用。

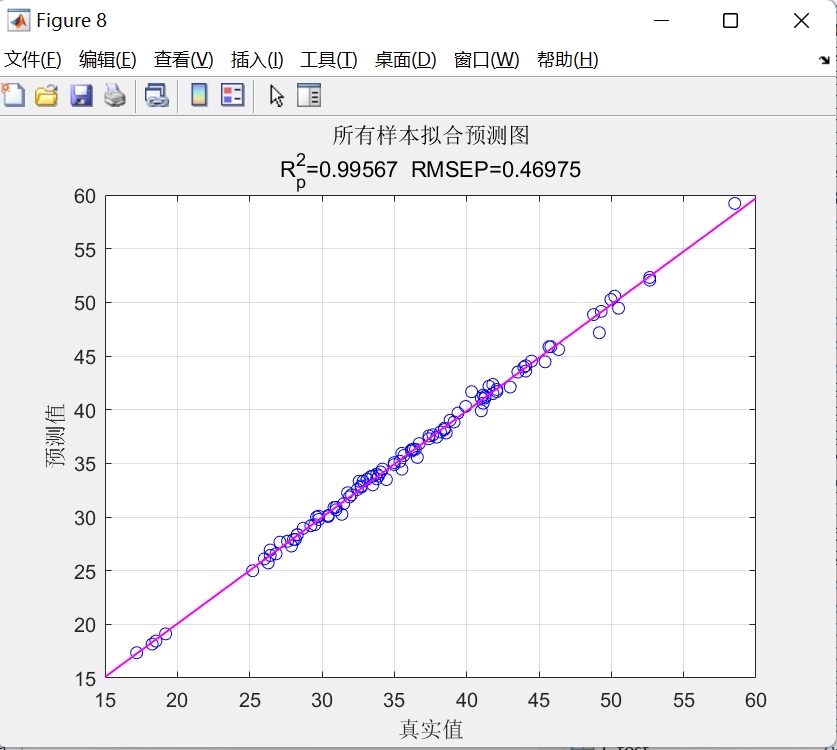
一、基本概念

高斯拟合（Gaussian fitting）又称正态分布拟合，是一种基于高斯函数（正态分布函数）的拟合方法。高斯函数通常具有一个峰值和两个对称的尾部，其数学表达式为：

f(x) = a  exp(-(x-b)^2 / (2c^2))

其中，a是峰值，b是均值（中心位置），c是标准差（宽度）。这三个参数就是高斯拟合需要求解的参数。

二、高斯拟合的原理

高斯拟合的原理是通过调整高斯函数的参数，使得该函数与原始数据点尽可能地吻合。这种拟合过程可以通过数学上的优化算法实现，例如最小二乘法等。在给定的一组数据点上，优化算法将调整高斯函数的参数（如a, b, c等），使得所有数据点到该函数的垂直距离的平方和达到最小。

三、高斯拟合的应用



信号处理：在信号处理中，高斯拟合常用于噪声信号的平滑处理和滤波操作，能有效减少数据噪声的干扰，帮助分析真实的数据规律。



统计学和概率论：在统计学和概率论中，高斯拟合用于估计和预测随机变量的分布情况，特别是在生物医学、经济预测等领域有着广泛的应用。



机器学习：在机器学习的模型构建过程中，常采用高斯分布模型对参数进行初始化和约束，保证模型稳定且鲁棒。此外，在一些异常值检测中也会使用到高斯拟合技术。



四、总结

高斯拟合是一种重要的数学工具，具有广泛的应用场景。通过了解其基本原理和掌握相关应用方法，我们可以在数据分析、机器学习等领域取得更好的成果。然而，不同的数据类型和问题需要采用不同的处理方法，选择合适的拟合方法和工具才能获得最佳的解决效果。同时也要注意其缺点，比如过度依赖样本的质量以及假设的正态分布与实际情况不符等问题。对于更复杂的问题或情况，我们需要灵活使用不同的技术和工具来进行分析和建模。