标题：有向完全图


内容：


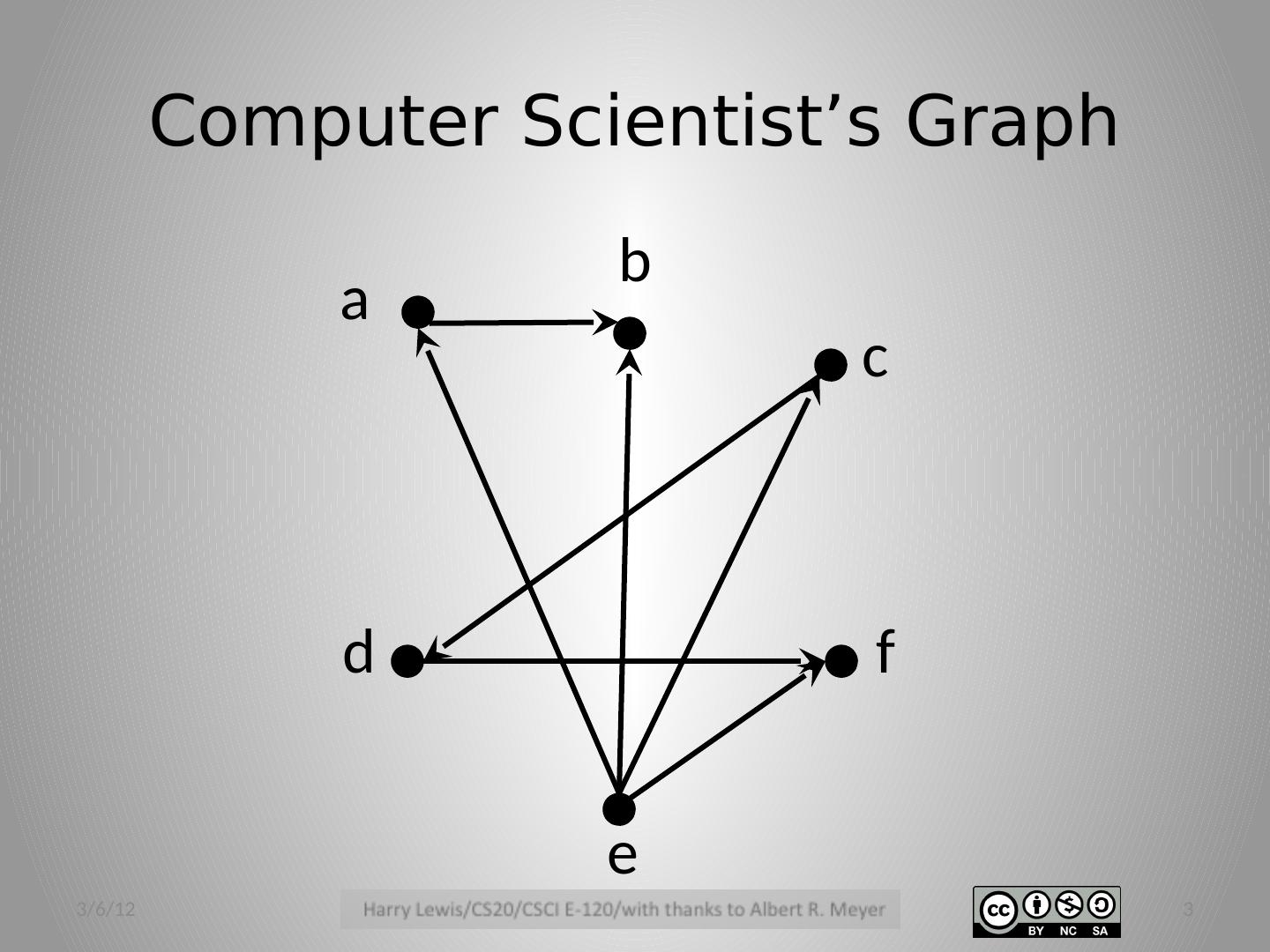
有向完全图是一个计算机领域的重要概念，常常被用来描述有向网络关系的一种形式。接下来，我将为您详细解析有向完全图的相关知识。

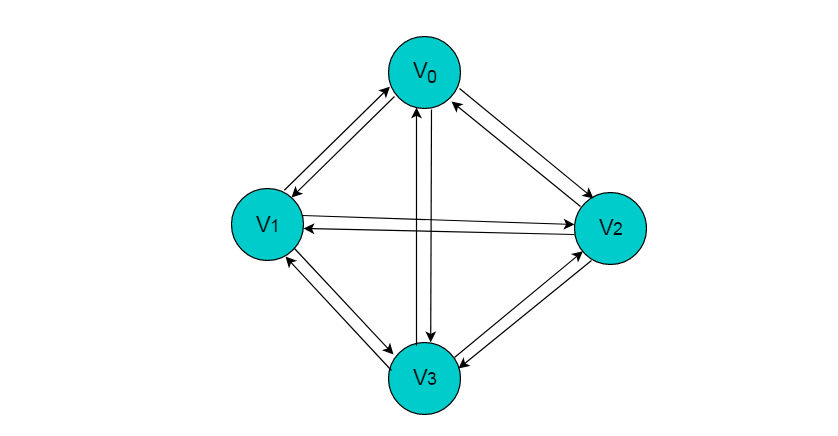
一、概念介绍

有向完全图是一种特殊的图，它包含了所有可能的有向边。具体来说，对于给定的n个顶点，有向完全图是一个图，其中每个顶点都与其他所有顶点之间存在一条有向边。也就是说，从任意一个顶点出发，都可以到达其他所有顶点。

二、有向完全图的特性


连通性：由于有向完全图中任意两个顶点之间都存在一条有向边，因此该图是连通的。
边的数量：在有n个顶点的有向完全图中，每条顶点都可以指向其他所有n-1个顶点，所以整个图中存在n*(n-1)条边。这也意味着任何无向的图都会在其所有无向化情况下呈现为一个无向完全图。
复杂性：随着顶点的增加，有向完全图的复杂度将显著增加。它可能会对分析造成一定困难，因此需要相应的计算机科学理论和方法进行支撑。

三、有向完全图的应用


描述关系网络：在计算机科学、社会网络分析等领域中，有向完全图常常被用来描述复杂的网络关系。例如，描述某个公司的员工关系、社交媒体用户的关系等。
搜索算法：在计算机中，利用有向完全图可以实现各种高效的搜索算法。比如Dijkstra算法等在复杂图论中发挥着重要作用。
网络分析与建模：通过对网络结构的详细分析和建模，可以更好地理解网络中各个元素之间的相互关系和影响。这有助于我们更好地进行网络优化和设计。

四、总结

综上所述，有向完全图是一种重要的图论概念，具有连通性、边的数量众多等特性。它在计算机科学、社会网络分析等领域有着广泛的应用。通过对有向完全图的研究和分析，我们可以更好地理解复杂的网络关系和相互影响，从而更好地进行网络设计和优化。

希望这篇文章能帮助您更好地理解有向完全图的概念和应用场景。如果有任何疑问或需要进一步解释，请随时向我提问。