一、z值计算公式的概念


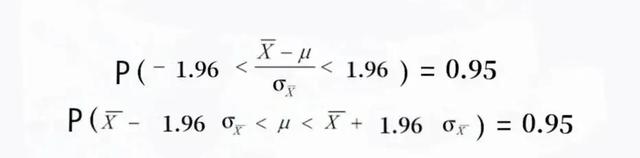
在统计学中，z值（Z-Score）是一个重要的概念，它常常被用来描述一个数值相对于平均值的距离。Z值表示了一个数据点在数据集分布中的位置，它可以帮助我们更好地理解数据的分布情况。


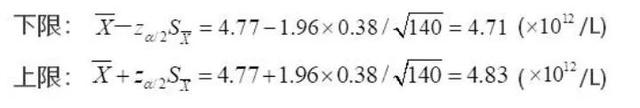
二、z值计算公式的具体形式

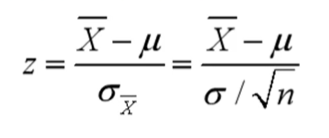
z值的计算公式为：z = (X - μ) / σ

其中，X是某一具体的数值，μ是数据的平均值，σ是数据的标准差。这个公式告诉我们如何根据一个具体数值、平均值和标准差来计算z值。

三、z值计算公式的应用场景

Z值计算公式在统计学中有着广泛的应用，例如在正态分布的假设下，我们可以利用z值来估计一个数值在数据集中所处的位置，以及计算一个特定的区间范围内的数值数量等。在质量管理和生产控制中，z值也常被用来描述生产过程中某个产品的离散程度和偏移情况。

四、z值计算公式的中文解读

我们可以通过具体的例子来进一步理解z值计算公式。假设我们有一组数据，其平均值为100，标准差为5。那么我们可以根据公式计算出每一个数值的z值。如果某个数值为110，那么它的z值为（110-100）/5=2。这意味着这个数值比平均值高了两个标准差。通过这种方式，我们可以对数据进行深入的分析和解读。

五、总结

总的来说，z值计算公式是一个非常有用的工具，它可以帮助我们更好地理解数据的分布情况和某一数值在数据集中的位置。在处理大量数据时，z值可以帮助我们快速地找到关键信息，并做出更准确的决策。希望这篇文章能够帮助你更好地理解z值计算公式及其应用。