一、文章标题


决定系数


二、文章内容

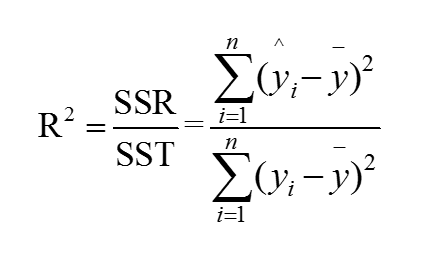
决定系数是统计学中常用的一个概念，尤其在多元回归分析中起着举足轻重的作用。了解并正确使用决定系数，能够帮助我们更准确地分析自变量与因变量之间的关系。下面就让我们来深入了解一下决定系数的含义、作用和计算方法。

1. 决定系数的定义

决定系数（Determination Coefficient，常简称为R²）是回归分析中用来描述模型拟合度的一个统计量。它表示的是自变量对因变量的解释程度，即模型中自变量对因变量的变化所贡献的比例。简单来说，就是模型中自变量对于因变量的可解释变异程度。

2. 决定系数的作用

（1）评估模型拟合度：决定系数能够很好地反映模型中自变量与因变量之间的关联程度。值越接近于1，说明模型中自变量对因变量的解释程度越高，即模型拟合度越好。

（2）判断自变量对因变量的影响程度：通过观察决定系数的值，我们可以判断出自变量对因变量的影响程度大小。如果决定系数较高，说明自变量对因变量的影响较大；反之则说明影响较小。

（3）模型优化：根据决定系数的值，我们可以对模型进行优化。例如，当发现模型的决定系数较低时，可以尝试引入新的自变量或改变模型的构建方式等，以提高模型的拟合度。

3. 决定系数的计算方法

决定系数的计算公式为R² = (SSR / SST) * 100%，其中SSR（回归平方和）和SST（总平方和）均来自回归分析中的计算。具体计算过程需要运用统计学软件或编程语言进行实现。需要注意的是，在计算过程中应遵循统计学原理和规则，确保数据的准确性和可靠性。

总之，决定系数是多元回归分析中一个非常重要的概念。了解其定义、作用和计算方法，有助于我们更好地运用多元回归分析来研究实际问题。在实践应用中，我们应该根据具体情况选择合适的模型和方法来计算决定系数，并对其结果进行合理分析和解读。