一、文章标题


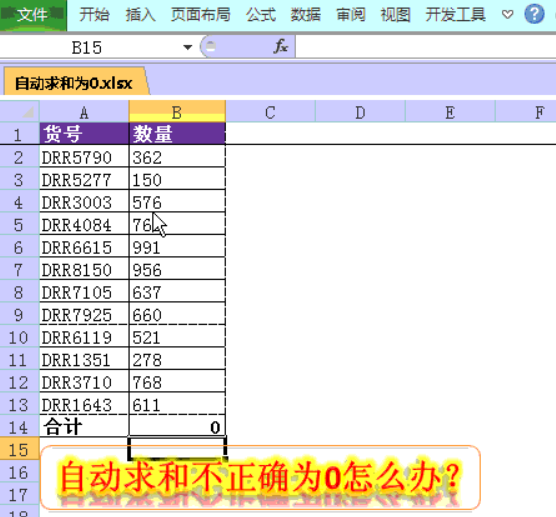
求和为什么是0？


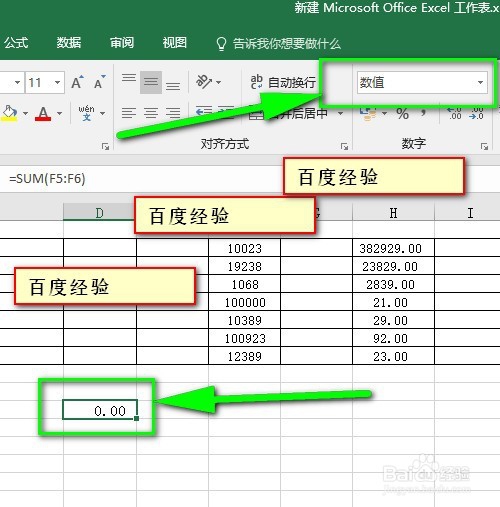
二、文章内容

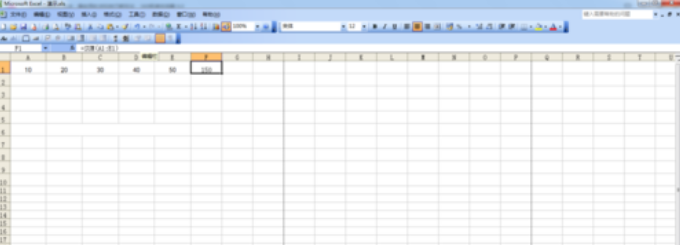
在数学中，求和为0的情况经常出现，尤其是在处理一些特殊的数学表达式和公式时。下面我们来探究一下求和为什么会出现为0的情况。

首先，我们来看一些基本概念。求和，通常指将一系列的数加在一起的过程。而在一些情况下，当我们对一系列数进行求和时，结果可能为0。这通常是因为这些数之间存在某种特定的关系或规律。

第一种情况：正负数相消。在数学中，正数和负数相加是常见的操作。如果在一系列数中，正数和负数的数量相等，那么它们的和就可能为0。例如，我们有一个数列：2，-3，4，-5...如果我们只取其中的前两个正数和后两个负数进行求和，那么结果就是（2+4）+（-3+5）= 9 - 3 = 6。但是如果我们把这个数列中的所有数都加起来，由于正负数数量相等，它们的和就可能为0。

第二种情况：线性空间中的向量求和。在向量空间中，存在一些特殊的向量称为零向量（即模长为0的向量），这个向量的坐标通常为零值或可互相抵消的值。对于一系列零向量，它们求和后通常也会为0。这种规律也被应用于高阶的线性空间和微积分中。

第三种情况：其它特定的公式或定理。在一些数学问题中，有些公式或定理告诉我们当某些特定条件下满足时，一个数学表达式的值就为0。比如余弦函数（cosine function）在某些特定角度上会得到-1或1这样的结果。而其他特定的求和公式如欧拉-麦卡托里尼（Euler-Maclaurin）公式或阿达马尔不等式（Adamaer's inequality）等也涉及到某些特殊情况下的求和结果为0的情况。

总结起来，求和为0的情况通常是因为所涉及的数之间存在某种特定的关系或规律，使得它们的和可以被相互抵消或者抵消为0。在实际的数学应用中，这种特殊现象也常常出现并有着广泛的应用价值。同时我们也需要明白的是，虽然我们可以在特定的情境下预测一些数列或者公式的和可能为0的情况，但这需要充分的数学知识来进行证明或推理才能得到结果。对于普通的情境而言，我们在理解它们时也应该具备一定的数学知识及敏锐的直觉思维才得以领悟到背后的原理及规律。