文章标题：函数拟合


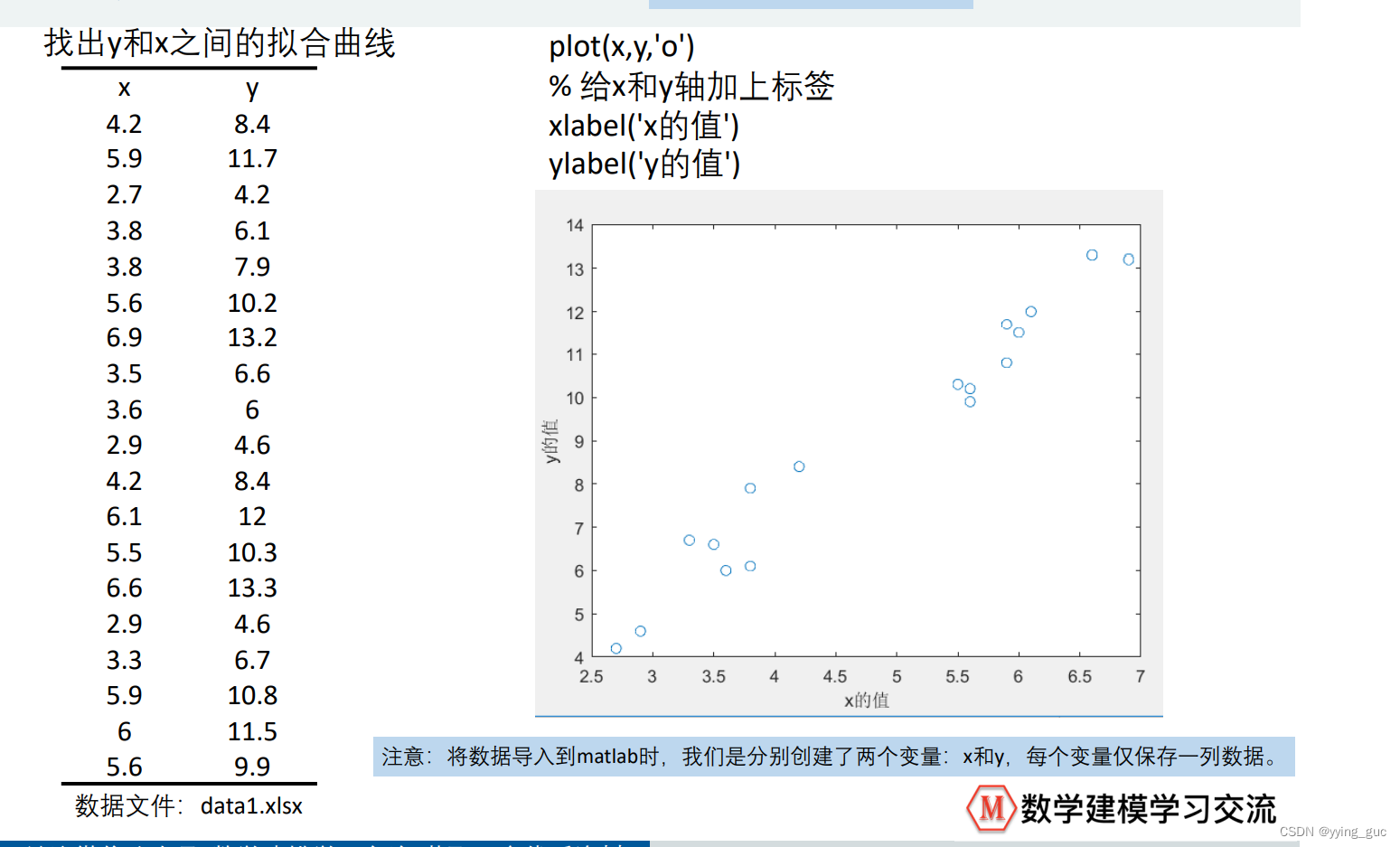
函数拟合是数据分析中常用的一种方法，它通过数学模型来描述数据之间的关系。在许多领域中，如物理、化学、生物、经济等，都需要进行函数拟合来分析数据。本文将介绍函数拟合的基本概念、方法以及应用场景。


一、函数拟合的基本概念

函数拟合是指通过选择合适的数学模型来描述一组数据之间的关系。这个数学模型通常是一个函数，它能够尽可能地接近原始数据，从而反映数据的变化趋势和规律。函数拟合的目的是为了更好地理解和解释数据，同时也可以用于预测和插值等应用场景。

二、函数拟合的方法



线性回归：线性回归是一种常用的函数拟合方法，它通过建立线性模型来描述自变量和因变量之间的关系。线性回归的优点是简单易懂，计算量小，适用于处理大量数据。



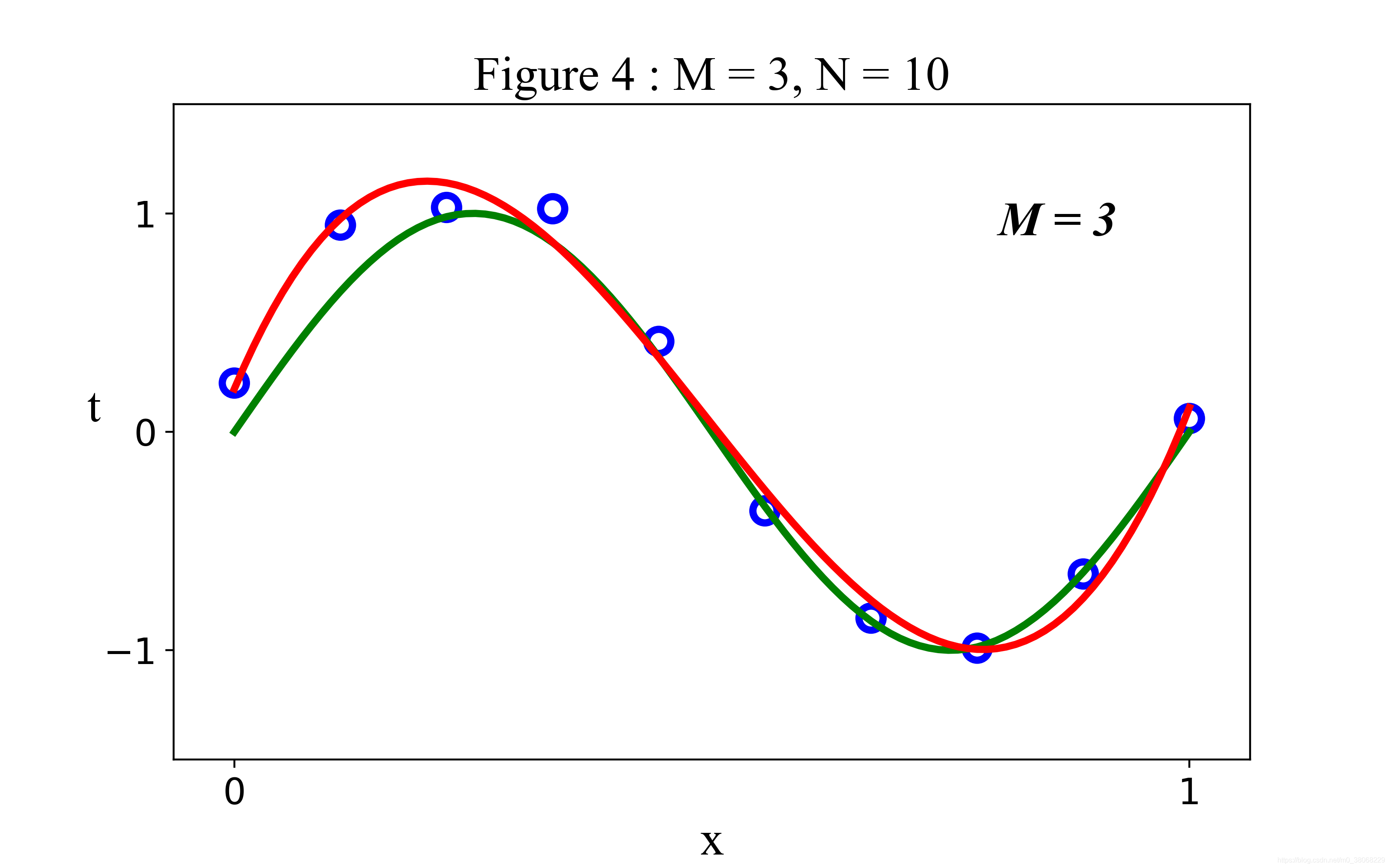
多项式回归：多项式回归是一种通过多项式函数来描述数据之间关系的拟合方法。多项式回归可以更好地描述非线性关系，但需要注意过拟合的问题。



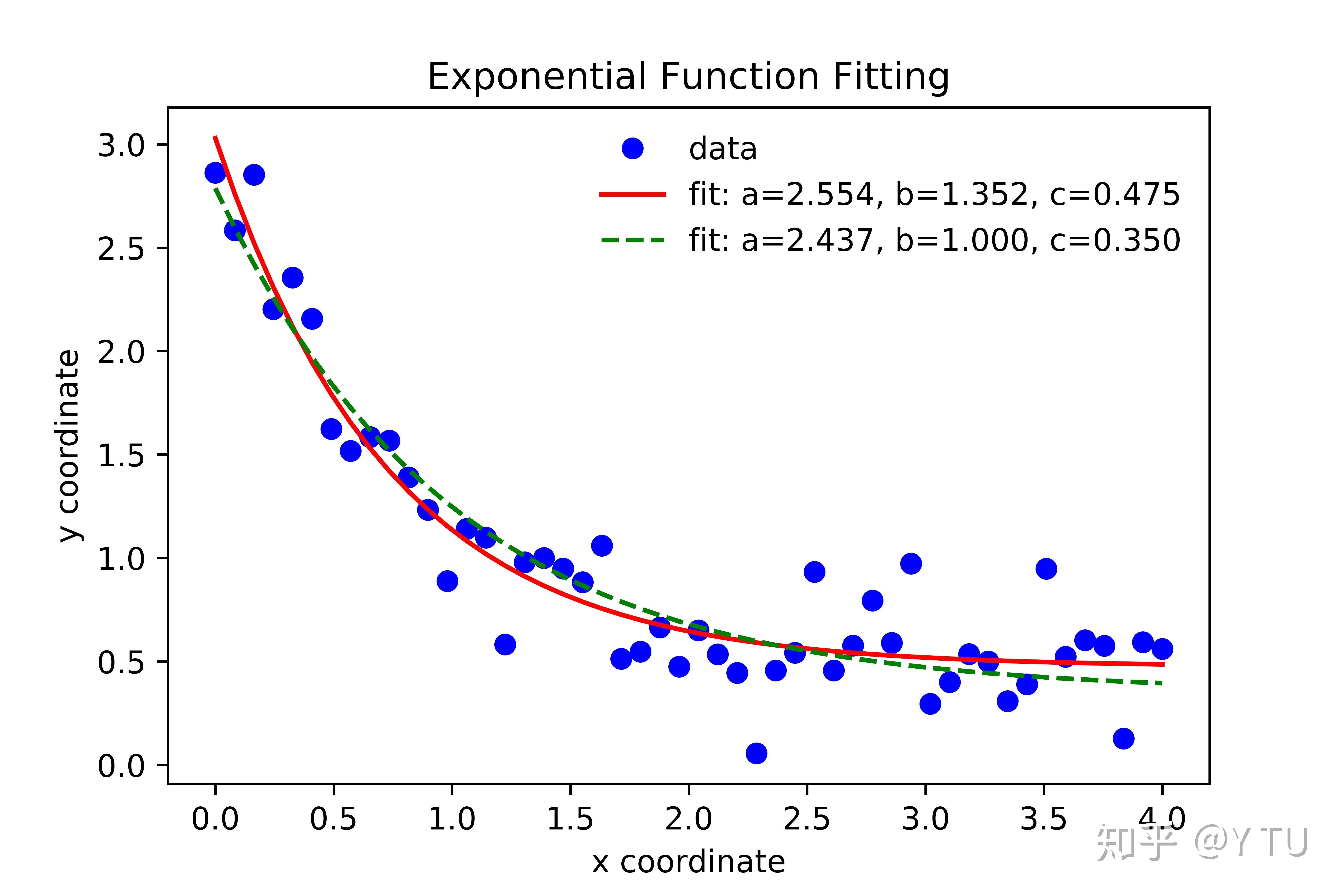
指数平滑法：指数平滑法是一种时间序列数据的处理方法，通过考虑历史数据的权重来对未来的趋势进行预测。



三、函数拟合的应用场景



物理实验：在物理实验中，可以通过函数拟合来描述实验数据的分布规律，从而更好地理解和解释实验结果。



金融市场：在金融市场中，函数拟合被广泛应用于股票价格、利率等金融数据的分析和预测。



生物医学：在生物医学领域中，函数拟合可以用于药物浓度的监测、疾病的发病率和死亡率分析等方面。



四、总结

函数拟合是一种重要的数据分析方法，它可以帮助我们更好地理解和解释数据，同时也可以用于预测和插值等应用场景。在实际应用中，我们需要根据数据的特性和需求选择合适的数学模型来进行拟合。同时，还需要注意过拟合的问题，避免模型过于复杂而失去对数据的解释能力。未来随着大数据和人工智能技术的发展，函数拟合将会得到更广泛的应用和改进。