一、代数的概念


代数学，是数学的一个重要分支，它研究的是数、结构、变化以及它们之间的关系。代数学的内容广泛，包括但不限于代数式、方程、函数等，具有极强的应用性和普遍性。


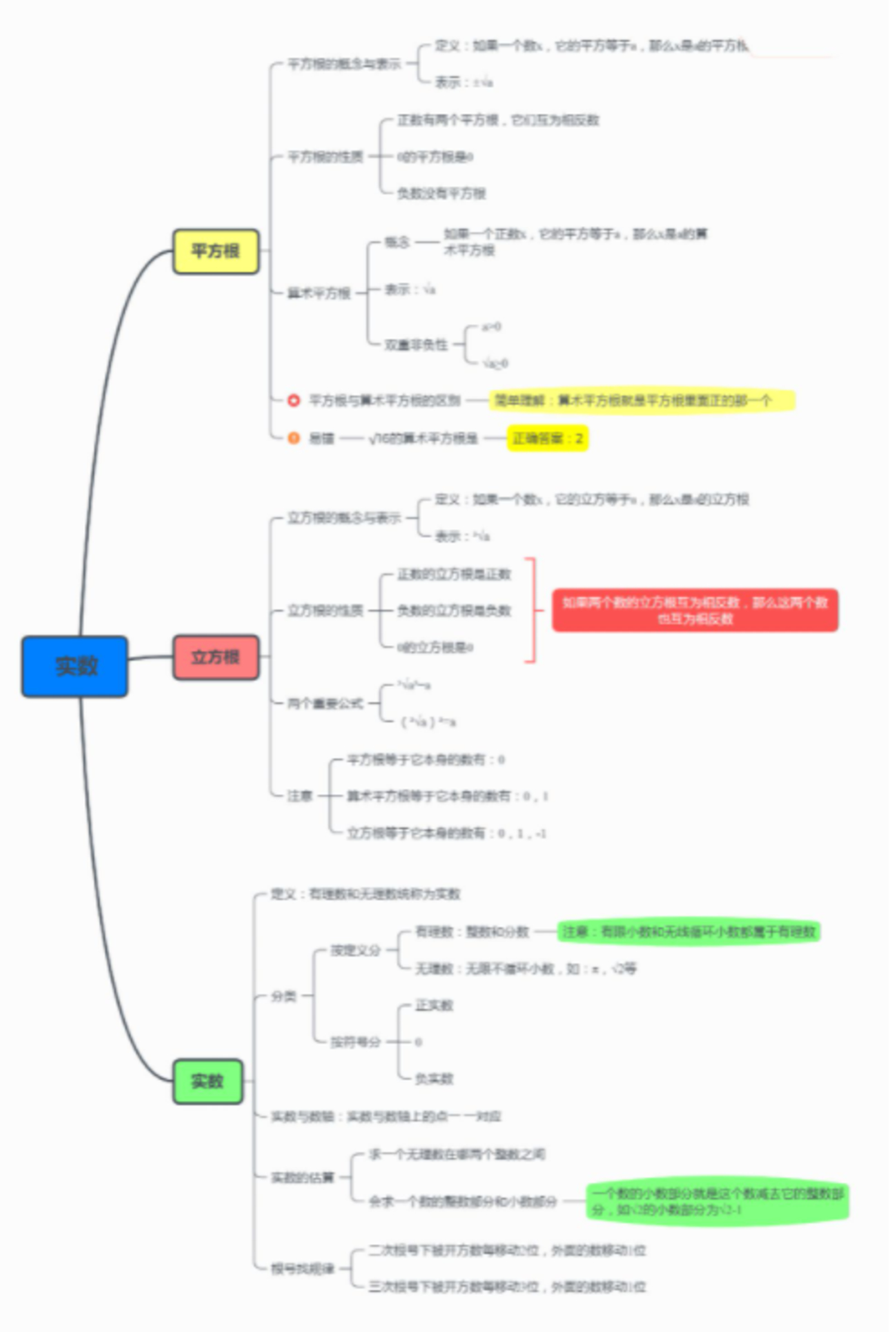
二、什么是代数？

定义：代数是数学的一个领域，研究各种数（如整数、有理数、实数、复数等）的性质以及这些数之间通过代数运算而产生的结构和规律。

代数的特点：



符号化：代数学的基本特点之一是符号化，如使用字母代替数字或其它未知量。这种符号化表示使得我们可以抽象地理解和研究数的性质，揭示各种关系。



公式和方程：代数不仅关心单独的数字，而且也关注更一般的结构和模式。如各种代数式、方程式以及各种特殊的公式和等式都是代数的研究对象。



变换性：通过加法、减法、乘法、除法等基本的算术运算和扩展的指数运算等代数运算，可以对式子进行变形，求解方程。



三、代数的基础知识



代数式：由数字、字母和运算符组成的数学表达式。如a+b、x^2等。



方程：将代数式用等号连接起来形成的数学关系式。如ax=b形式的线性方程，或是更高次数的多项式方程等。



函数：一个量随着另一个量的变化而变化的关系。如一次函数y=kx+b中，k和b都是参数，k决定了函数的斜率，b决定了与y轴的交点位置。



四、代数的作用与价值

在现代数学的大家族中，代数无疑是许多学科之间的一座桥梁。在日常生活和学习中，无论是复杂的经济分析、科学实验数据的分析还是逻辑推理和问题的解决都离不开代数的帮助。在科学研究方面，代数也具有举足轻重的地位，为众多领域的深入探索提供了强有力的数学工具。

总之，代数学作为数学的一个重要分支，它以抽象的方式描述了数与数之间的关系和规律，是理解数学世界的重要工具之一。无论是对于专业学者还是对于普通人来说，了解代数的概念都是极其有意义的。希望上述的讲解能够帮助您对代数有一个更加深入的了解和认识。