一、文章标题


什么是齐次方程？

二、文章内容

齐次方程是一个线性代数领域中的概念，广泛用于微分方程、矩阵计算等学科。了解齐次方程的基本概念及其应用对于深入学习这些学科具有非常重要的作用。下面将为大家详细解释齐次方程是什么。


齐次方程的定义

齐次方程通常是指一类线性方程组，它的一个重要特点是：在所有的未知数（变量）之前都有一个对应的系数。在这个线性方程组中，每个变量的幂次数相等且均不含零次项（常数项）或者变量的零次项被设置为零（即在多项式方程中无独立的常数项）。这种特殊的线性方程组，就被称为齐次方程。


齐次方程的常见形式

在数学领域，齐次方程主要涉及在多维空间中的几何运算，因此它通常表现为一系列多项式或函数等式。例如，在微分方程中，我们常常会遇到形如 y' + 2xy = 0 的齐次方程，其中 y 是未知数，x 是自变量，y' 是 y 对 x 的导数。此外，在矩阵计算中，我们也经常遇到涉及矩阵和向量的齐次方程。


齐次方程的解法

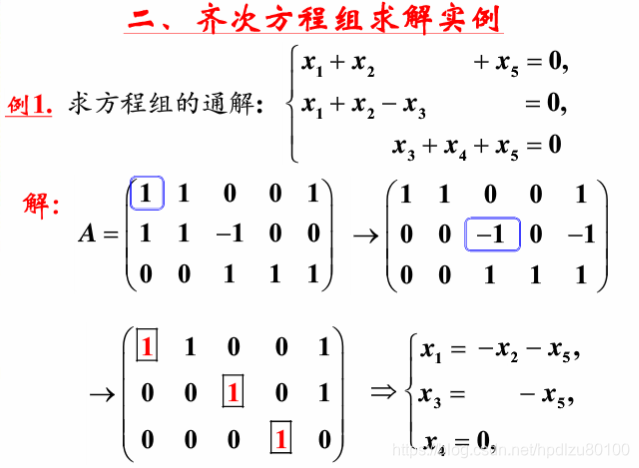
对于齐次方程的解法，我们通常使用线性代数中的矩阵运算或高阶微分等手段。例如，我们可以利用线性变换、特征值与特征向量等方法求解微分形式的齐次方程；而对于更一般的线性方程组，我们可以通过行列变换和消元法等方法来求解。对于非线性的情况，我们需要通过数值方法进行迭代求解。


齐次方程的应用

齐次方程在科学计算、工程设计等领域具有广泛的应用。例如，在电路分析中，我们可以利用齐次方程来描述电流和电压之间的关系；在化学平衡理论中，我们可以利用齐次方程来描述化学反应速率和浓度的关系；在计算机科学中，齐次方程也被用于机器学习算法和人工智能等重要领域。

综上所述，齐次方程是一个非常重要的概念，它在数学和其他许多领域中都有着广泛的应用。理解齐次方程的定义、性质以及解法将有助于我们更好地解决实际问题和推动科学技术的发展。因此，掌握和运用好齐次方程是非常有意义的。