旋转因子


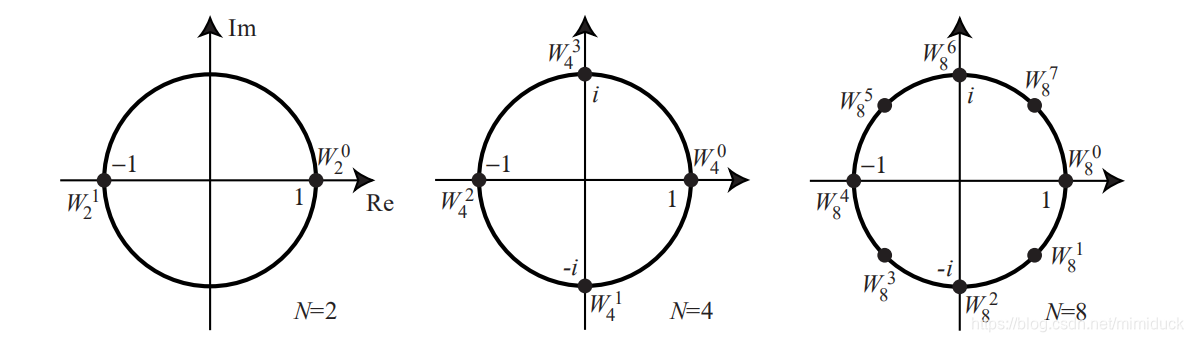
在数学和物理领域中，旋转因子是一个重要的概念，它涉及到复数、向量和三维空间旋转等多个方面。本文将简要介绍旋转因子的基本概念、性质及其在各个领域中的应用。


一、旋转因子的基本概念

旋转因子通常以复数的形式出现，它是一个与角度和单位圆相关的数学对象。在复数平面上，我们可以将旋转因子看作是绕原点进行旋转的向量。在三维空间中，旋转因子则与三维向量的旋转有关。

二、旋转因子的性质

旋转因子具有以下性质：


周期性：旋转因子在单位圆上具有周期性，即每旋转一周回到原点。
角度依赖性：旋转因子的值与旋转的角度有关，不同的角度会产生不同的复数值。
模长为1：旋转因子的模长始终为1，表示其长度始终保持不变。

三、旋转因子在各个领域的应用


物理学：在量子力学中，旋转因子被用来描述粒子的波函数，以及粒子在空间中的运动和变换。此外，在电磁学和光学中，旋转因子也被用来描述光波的传播和偏振状态。
数学：在复数分析和向量分析中，旋转因子被用来描述复数和向量的旋转操作。此外，在矩阵运算中，旋转因子可以用于构造旋转变换矩阵，实现三维空间的旋转操作。
工程学：在机械工程和电气工程中，旋转因子被广泛应用于电机控制、机器人运动规划和信号处理等领域。通过使用旋转因子，可以实现对机械系统和电气系统的精确控制和优化。

四、总结

旋转因子是一个重要的数学和物理概念，它涉及到复数、向量和三维空间旋转等多个方面。通过研究旋转因子的基本概念和性质，我们可以更好地理解其在各个领域中的应用。未来随着科技的不断发展，旋转因子将在更多领域发挥重要作用，为人类的发展和进步做出贡献。