正交是什么意思
正交，这个词在数学和物理学中常常出现，特别是在向量空间和线性代数中。要理解正交，首先得明白向量和它们之间的关系。


正交的定义


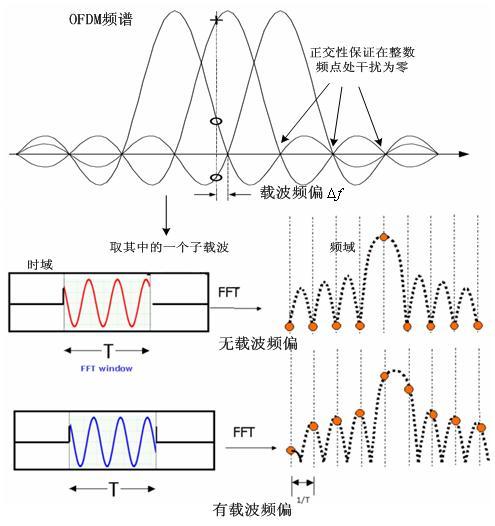
在数学中，两个向量是正交的，如果它们的点积（内积）为零。换句话说，如果两个向量的方向完全垂直，那么这两个向量就是正交的。在几何上，这意味着一个平面上的一条直线与该平面的一个直角边垂直。

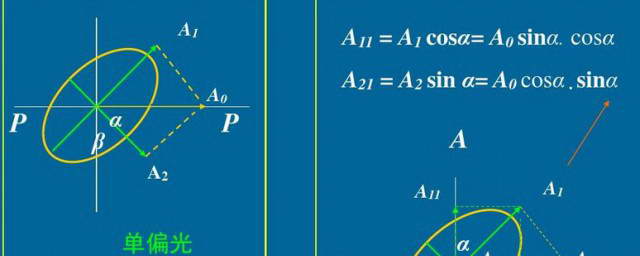
正交在向量空间中的意义

在向量空间中，正交是一个非常重要的概念。当我们在一个二维或三维空间中讨论时，这个概念更为明显。当我们在谈论平面的X和Y轴或者球面的θ和r（纬度、半径）这样的两个向量时，我们可以称这两个轴向量是正交的，因为它们互相垂直，一个指向点沿该方向并投射在这个方向上的全部单位矢量不会影响到另一个轴上的矢量值。

正交与矩阵的关联

在矩阵和线性代数中，正交矩阵是重要的工具。如果矩阵A的转置与它自身相乘得到的结果是单位矩阵（即乘以矩阵A本身或其转置之后回不到零的每个元素的乘积是该元素的模），那么矩阵A就被称为正交矩阵。对于这些矩阵，任意两个行或列向量的外积等于0，这也说明他们正交于对方。

物理意义与案例

物理中的矢量描述包括正交、分量的概念和欧拉运动描述方程（考虑坐标系的欧拉运动与静止时刻和活动状态等）。例如，在物理学中，力、速度、加速度等矢量都可以通过正交分解来分析其分量，从而更方便地计算它们的合成和分解。

总结

正交是一个重要的概念，在数学、物理和其他领域都有广泛的应用。它描述了向量之间的一种特殊关系，即它们之间完全垂直。通过正交的概念，我们可以更好地理解向量空间、矩阵和物理中的矢量分析等概念。希望这篇文章能帮助你更好地理解正交的含义和应用。