一、文章标题


Sympy库简介与应用


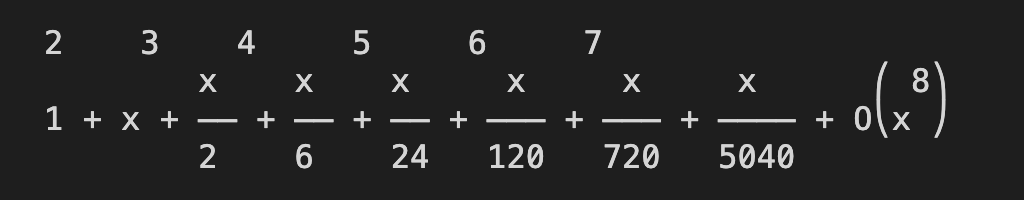
二、文章内容

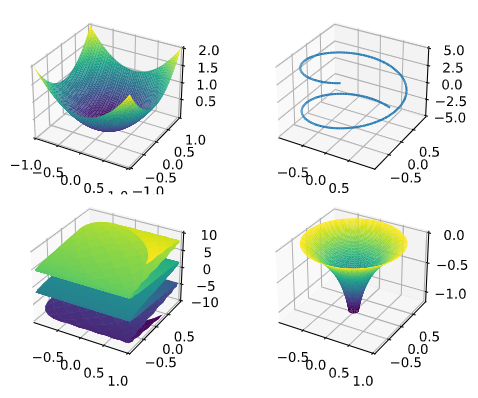
随着科学技术的飞速发展，Python已经成为众多科研工作者与数据分析师必备的编程语言之一。而sympy则是Python中一个强大的数学符号计算库，能够处理包括代数运算、微积分、离散数学等领域的数学问题。本文将简单介绍sympy库的基本概念、特点以及应用场景。

一、sympy库的基本概念

sympy是一个Python的符号计算库，它能够进行精确的数学运算，包括代数运算、微积分、离散数学等。在sympy中，所有的变量都被视为符号变量，即它们代表的是未知数或表达式中的变量。sympy通过符号计算，可以自动推导数学公式和定理，从而帮助我们解决复杂的数学问题。

二、sympy库的特点


符号计算：sympy库支持精确的符号计算，能够处理复杂的数学问题。
丰富的函数库：sympy库包含了丰富的函数库，能够进行代数运算、微积分等计算。
可读性高：在sympy中，代码易于理解且结构清晰，可以提高开发者的开发效率。
可定制性：sympy库提供了丰富的API接口，可以根据用户需求进行定制化开发。

三、sympy库的应用场景


代数运算：sympy可以用于进行代数运算，如多项式展开、因式分解等。
微积分：sympy可以用于进行微积分运算，如求导数、积分等。在科学研究和工程应用中，微积分是不可或缺的一部分。
物理引擎：在物理引擎中，sympy可以用于自动推导物理公式和定理，提高开发效率。
数据分析：在数据分析中，sympy可以用于进行统计量的计算和预测等任务。

四、实例展示

以一个简单的多项式求导为例，展示如何使用sympy进行计算。首先需要导入sympy库中的符号和diff函数，然后定义一个多项式表达式并使用diff函数求导数。具体代码如下：

from sympy import symbols, diff
x = symbols('x')  # 定义符号变量x
expr = x**2 + 3*x + 2  # 定义多项式表达式x^2 + 3x + 2
derivative = diff(expr, x)  # 对多项式表达式求导数
print(derivative)  # 输出导数结果为2*x + 3
以上就是使用sympy进行多项式求导的简单示例。通过这个例子可以看出，sympy可以帮助我们进行精确的数学运算，并且提供了丰富的函数库和API接口供我们使用。在科学研究和工程应用中，我们可以充分利用sympy的功能来解决各种复杂的数学问题。

总结：本文简单介绍了sympy库的基本概念、特点和应用场景，并通过一个简单的示例展示了如何使用sympy进行多项式求导。在实际应用中，我们可以根据具体需求选择合适的函数和算法来处理各种复杂的数学问题。