文章标题：取整函数图像


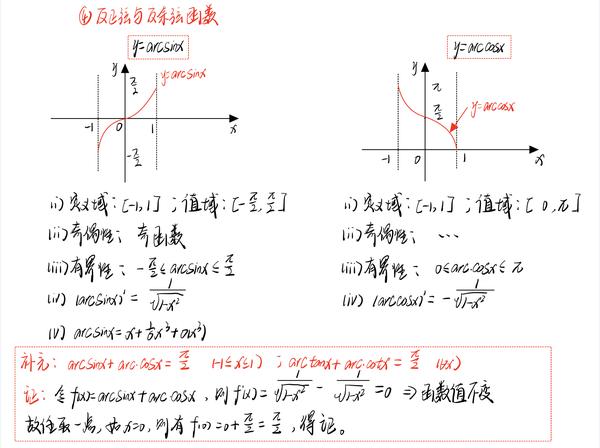
一、引言


在数学中，取整函数是一种非常常见的函数，其图像的形状和特性在各种领域有着广泛的应用。本文将详细介绍取整函数的定义、性质以及其图像的绘制方法。

二、取整函数的定义与性质

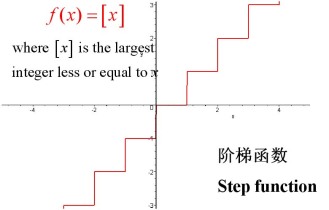
取整函数，顾名思义，是一种将实数或复数取整的函数。在数学上，取整函数可以表示为对任意实数x，取其整数部分。这种函数在数学分析、计算机科学等领域有着广泛的应用。

取整函数具有一些重要的性质。首先，它的值域是整数集，即对于任意实数输入，输出结果总是整数。其次，取整函数具有单调性，即当输入值增大时，输出值也相应增大。此外，取整函数还具有连续性和周期性等特性。

三、取整函数图像的绘制

要绘制取整函数的图像，我们可以借助一些数学软件或编程语言来实现。下面以Python语言为例，介绍一种简单的绘制方法。

首先，我们需要了解取整函数的数学表达式。取整函数的表达式可以根据不同的取整方式而有所不同，但最常见的有“向下取整”和“四舍五入”两种方式。这里我们以“向下取整”为例进行说明。

在Python中，我们可以使用matplotlib库来绘制函数图像。首先，我们需要导入必要的库和模块，并定义取整函数的表达式。然后，我们可以使用matplotlib的plot函数来绘制函数图像。具体步骤包括设置坐标轴范围、绘制函数曲线、添加图例和标签等。

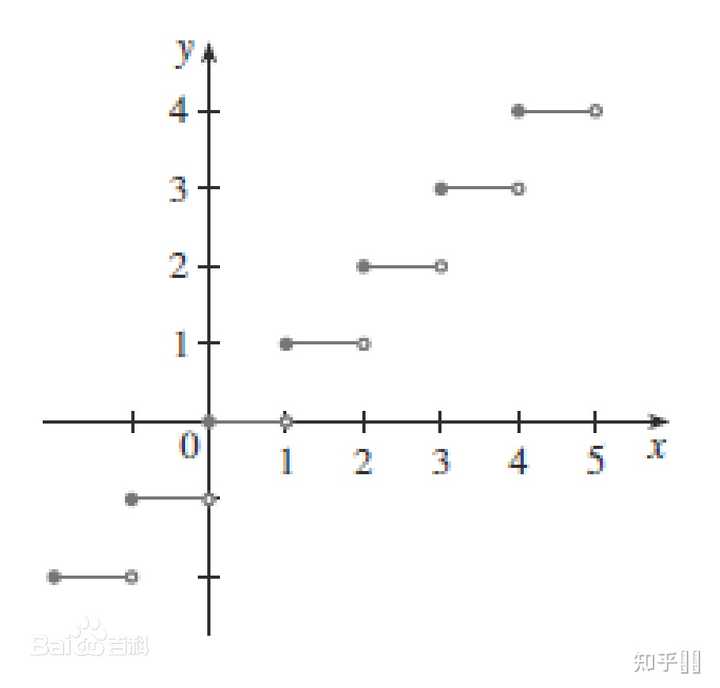
通过绘制取整函数的图像，我们可以更加直观地了解其性质和特点。例如，我们可以观察到取整函数在整数点处的跳跃现象，以及其在不同区间内的变化规律等。

四、结论

取整函数是数学中一种重要的函数类型，其图像的形状和特性对于理解和应用该函数具有重要意义。通过本文的介绍，我们了解了取整函数的定义、性质以及其图像的绘制方法。希望这些内容能够帮助读者更好地理解取整函数的相关知识。

在实际应用中，取整函数广泛应用于数学分析、计算机科学、物理学等领域。例如，在计算机科学中，取整函数可以用于处理浮点数运算、图像处理等问题；在物理学中，取整函数可以用于描述物理量的取值范围、周期性等现象。因此，掌握取整函数的相关知识对于提高我们的数学素养和应用能力具有重要意义。