一、单位向量


在数学和物理中，单位向量是一个非常重要的概念。它是一个具有方向和大小的向量，其长度为1。下面我们将从定义、性质、应用等方面来介绍单位向量。

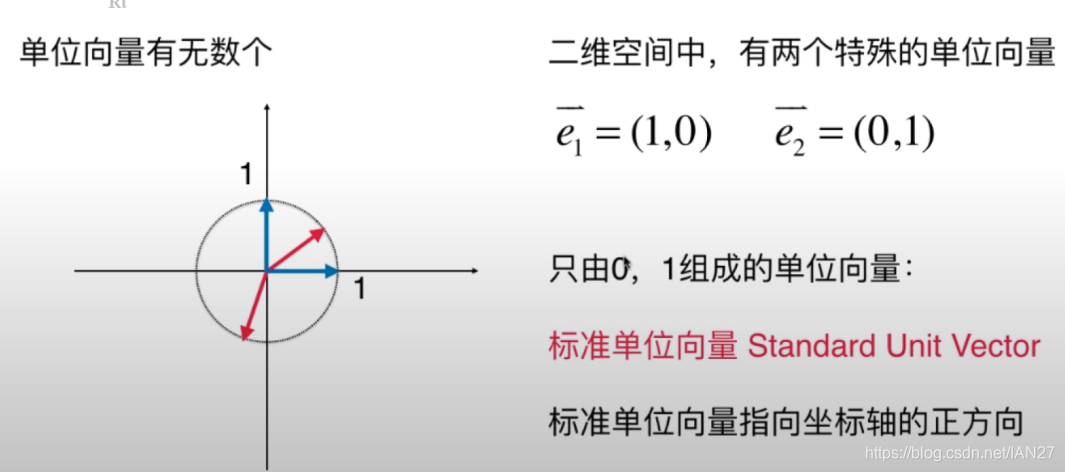
一、单位向量的定义

单位向量是指模长为1的向量。在二维空间中，单位向量可以表示为一个点（坐标）在X轴和Y轴上的投影的比值。在三维空间中，单位向量除了表示X轴和Y轴的投影之外，还表示了Z轴的投影。

二、单位向量的性质


模长为1：单位向量的模长总是等于1，这是其最基本的性质。
方向性：单位向量不仅具有大小，还具有方向性。方向相同但大小不同的两个向量，它们的单位向量是不同的。
归一化：一个向量可以通过除以它的模长来得到其单位向量。这个过程被称为向量的归一化。

三、单位向量的应用


物理中的应用：在物理学中，单位向量常常用于描述物理量的方向和大小，如力、速度等。例如，在力学中，力的方向和大小可以用一个单位向量来表示。
数学中的应用：在数学中，单位向量也扮演着重要的角色。例如，在空间解析几何中，单位向量可以用来表示方向向量，从而方便地描述空间中的各种几何关系。
计算机图形学中的应用：在计算机图形学中，单位向量常常用于表示法线、切线等几何量，是计算机图形学中不可或缺的一部分。

四、总结

以上就是关于单位向量的介绍。通过本文的介绍，我们可以看出单位向量在数学、物理、计算机图形学等多个领域都有广泛的应用。因此，理解和掌握单位向量的概念及其应用是非常重要的。

此外，需要注意的是在实际应用中，我们应该根据具体情况来选择是否使用单位向量。有时我们需要对向量的方向和大小进行精确的描述和分析，这时使用单位向量可以大大简化我们的计算和分析过程。同时，我们还需要注意单位向量的方向性，避免出现方向错误的情况。

总之，单位向量是一个非常重要的概念，它不仅具有基本的数学性质，而且在多个领域都有广泛的应用。因此，我们应该认真学习和掌握它的概念及其应用方法。