一、文章标题
解析函数

二、文章内容
在数学中,函数是一种非常重要的概念,而解析函数则是函数中一种特殊的类型。解析函数指的是在复数域内,每个点都存在一个定义好的值,且这些值是连续的。下面我们将从定义、性质、应用等方面来解析函数。
一、定义
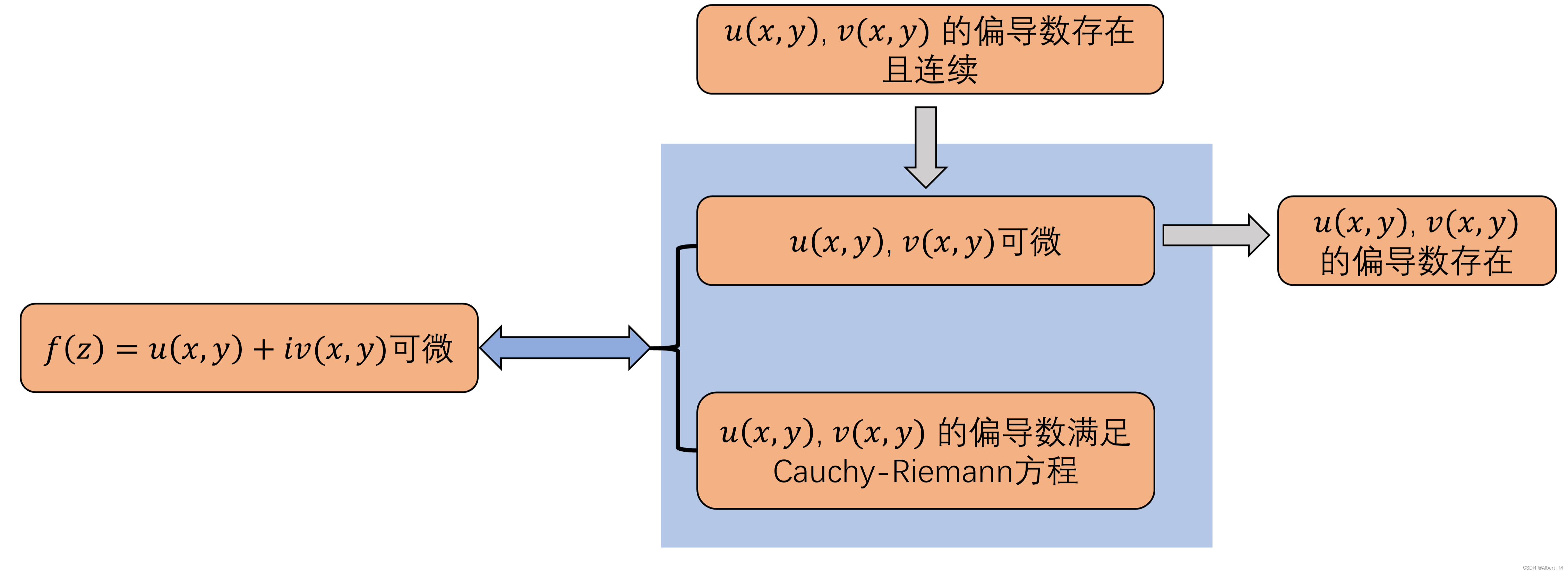
解析函数是指在复数域内,对于每个点都有定义且其值连续的函数。它不仅仅可以表示在实数范围内的数学对象,还能表示一些物理和几何方面的关系。此外,与普通的函数不同,解析函数的每一个点都有一个收敛的Taylor级数或Laurent级数表示,使得其在各种问题中的应用变得更加方便。
二、性质
解析函数在数学中有许多独特的性质。例如,其极点个数与给定的开区域上无穷点重数的数目之间有直接的关系,同时还存在幂级数和开尔文的分布律等规律。由于它有着在各个领域应用中的重要性,使得其在物理、经济和计算机科学等多个领域有着广泛的应用。
三、应用
-
物理学中的应用:解析函数在物理学中扮演着非常重要的角色。比如在电路分析中,电流、电压和功率都可以通过解析函数进行描述和计算。此外,在量子力学、热力学等物理领域中也有广泛的应用。
-
计算机科学中的应用:在计算机科学中,解析函数也被广泛应用。例如,在图形处理中,可以利用解析函数来描述各种复杂的形状和结构;在机器学习中,也可以利用解析函数来建立各种复杂的模型和算法。
-
经济学中的应用:在经济学中,解析函数也被用来描述各种经济现象和规律。例如,通过建立各种经济模型和函数关系,可以预测未来的经济走势和变化趋势。
总之,解析函数是数学中一个非常重要的概念,它具有许多独特的性质和应用价值。无论是物理、计算机科学还是经济学等领域,都需要用到解析函数的原理和方法来描述和解决各种问题。因此,我们应该深入学习和掌握解析函数的原理和方法,为解决实际问题提供更多的思路和方法。
标签:
- 解析函数
- 复数域
- 定义
- 性质
- 应用
- 数学模型

