齐次式是什么
在数学中，齐次式是一个在经过运算或转换后仍然保持某种特性的表达式。其特点是在变换时，所有的变量（或未知数）都会乘以同一个系数或被置于相似的指数中。接下来我们将一起了解齐次式的具体定义、应用场景和特点。


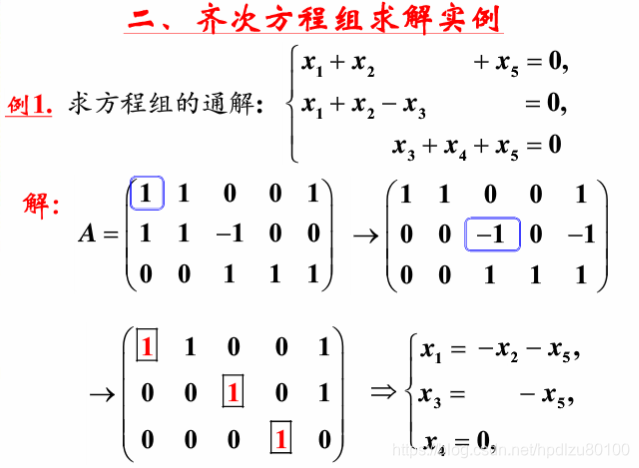
一、齐次式的定义
齐次式（Homogeneous Polynomial）是一个多项式，其每一项的次数都相同。这里的“次数”指的是每一项中所有变量的指数之和。例如，对于多项式x^2y + 2xy^2，每一项的次数都是2（第一个项x^2y中x的指数是2，y的指数是1；第二个项2xy^2中x的指数是1，y的指数是2）。因为每个项的次数相同，所以这是一个齐次多项式。


二、齐次式的应用场景
齐次式在数学、物理和工程等多个领域都有广泛的应用。例如，在物理学中，齐次式常用于描述具有比例关系的物理量之间的关系；在数学中，齐次式常用于代数方程和微分方程的求解等。此外，在经济学、化学等领域也有其应用。

三、齐次式的特点

全部项的次数相同：这是齐次式最显著的特点，每一项的次数必须相同。
易于处理：通过变换或化简，我们可以更容易地找到齐次式的解或解集。
广泛应用：齐次式在多个领域都有广泛的应用，如代数、微分方程、物理等。

四、齐次式的示例
让我们看一个简单的齐次式例子：x^3 + y^3 + z^3。这是一个三次齐次多项式，因为每一项的次数都是3。在物理中，这个形式常用于描述具有对称性的物理系统。

五、总结
总的来说，齐次式是一个在数学和物理等领域中广泛应用的数学工具。它具有特定的形式和特性，可以用于描述具有特定关系的物理量或解决特定类型的数学问题。希望这篇文章能帮助你更好地理解齐次式的概念和应用。

以上内容为简要说明，若要详细阐述这一主题需要更长的篇幅。当然如果有更多疑问或者想要深入学习这方面的知识可以进一步提问或者查询相关资料文献进行了解。