一、文章标题


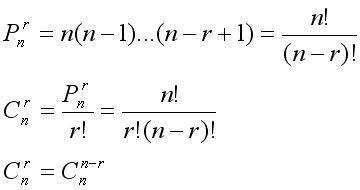
排列数公式


二、文章内容

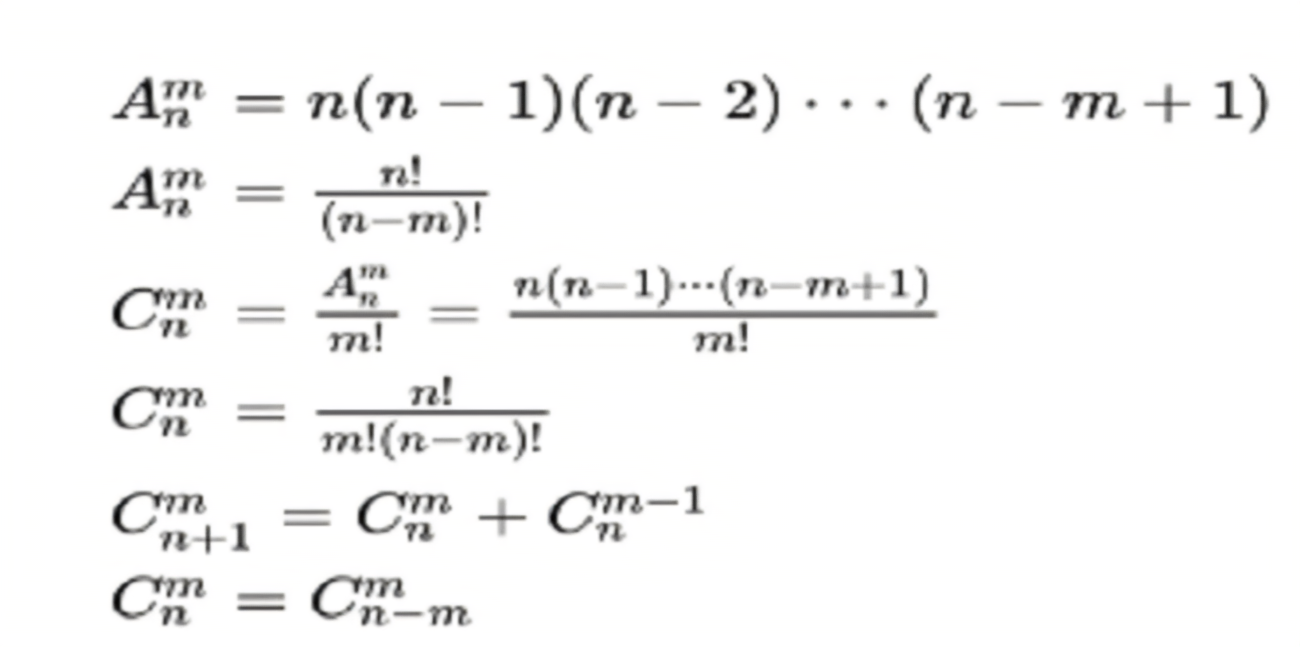
排列数公式是数学中非常基础且重要的概念，它常常被用于计算一组对象的所有可能排列数。本文将详细介绍排列数公式的定义、性质以及应用场景。

1. 排列数公式的定义

排列数是指从n个不同元素中取出m（m≤n）个元素按照一定的顺序进行排列的个数。排列数公式通常用符号P(n, m)表示，其计算公式为：

P(n, m) = n × (n-1) × ... × (n-m+1)

这个公式表示从n个不同元素中取出m个元素进行排列的所有可能情况。当m=n时，表示所有元素的排列数，也称为全排列数。

2. 排列数公式的性质

（1）P(n, m)是一个正整数，其值随m的增大而迅速增加；
（2）P(n, n)是所有可能的全排列数，具有较大的计算量；
（3）对于固定的n和m，P(n, m)只与n和m的取值有关，与其他无关的参数无关；
（4）P(n, m)具有对称性，即P(n, m) = P(m, n)。

3. 排列数公式的应用场景

（1）在数学领域，排列数公式被广泛应用于组合数学、概率论和图论等领域；
（2）在计算机科学中，排列数公式可以用于算法设计和性能分析，如全排列算法等；
（3）在现实生活中，排列数公式也被广泛运用于统计学、生物信息学、医学等领域。

三、总结

本文介绍了排列数公式的定义、性质和应用场景。通过学习和掌握这个重要的数学概念，我们可以更好地理解和应用它在各个领域中的实际运用。排列数公式是一个非常有用的工具，它不仅可以帮助我们计算各种组合的个数，还可以帮助我们更好地理解数学中的基本概念和原理。同时，通过对排列数公式的深入学习和研究，我们还可以进一步提高自己的数学素养和思维能力。