实数集是什么
一、概述


实数集，通常用大写字母R表示，是数学中一个非常重要的概念。它包含了所有实数，包括有理数和无理数。实数集是数学领域中一个非常基础且广泛的概念，它不仅在初等数学中有所涉及，在高等数学、物理学、工程学等领域也有广泛应用。


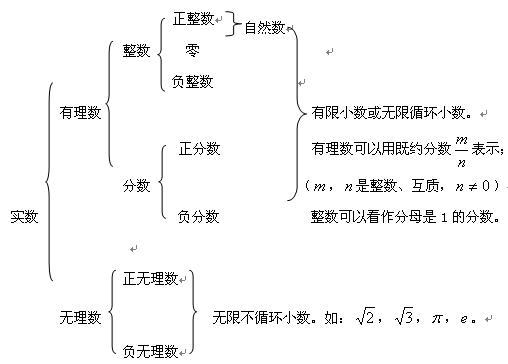
二、实数的定义与分类

实数可以从不同角度进行分类。按照性质来分，实数可以分为有理数和无理数。有理数是可以表示为两个整数之比的数，而无理数则无法用两个整数之比来表示，如圆周率π和自然对数的底数e等。

再进一步细分，有理数又可以分为整数、正整数、负整数、正负小数等。无理数则主要是一些特定的常数和无限序列。

三、实数集的性质与特点

实数集有以下几个重要性质：


顺序性：实数集是有序的，每一个实数都可以通过大小关系进行排列。
完备性：实数集是完备的，即所有收敛的数列在实数集中都有唯一的极限值。
稠密性：实数集在数轴上任意两点之间都存在实数。这一性质使得实数集具有很高的计算和逼近精度。

四、应用实例

在各个学科领域中，实数集都有广泛的应用。比如：


数学：在数学分析、代数和几何等领域，实数集提供了对抽象数学问题进行处理的基础框架。
物理学：物理中的力学、电磁学、热学等都需要用到实数集的概念和性质。
计算机科学：在计算机图形学、数值计算等领域，实数集的精确性和计算性都得到了广泛的应用。

五、总结

实数集作为数学中的一个基础概念，具有广泛的应用价值。它不仅在数学领域有着重要的地位，还在其他学科领域如物理学、计算机科学等有着广泛的应用。因此，了解和掌握实数集的概念和性质，对于学习数学和其他相关学科的人来说都是非常重要的。

希望这篇文章能够帮助您更好地理解实数集这一基础概念。如果还有其他问题或需要进一步的解释，请随时告诉我。