文章标题：向上取整公式


在数学中，取整是一个常见的概念，它涉及到将一个数四舍五入到最接近的整数。然而，有时候我们也需要向上取整，即将一个数取到大于或等于该数的最小整数。这在实际生活和科学研究中非常有用。下面我们来探讨一下向上取整的公式。


一、向上取整的基本概念

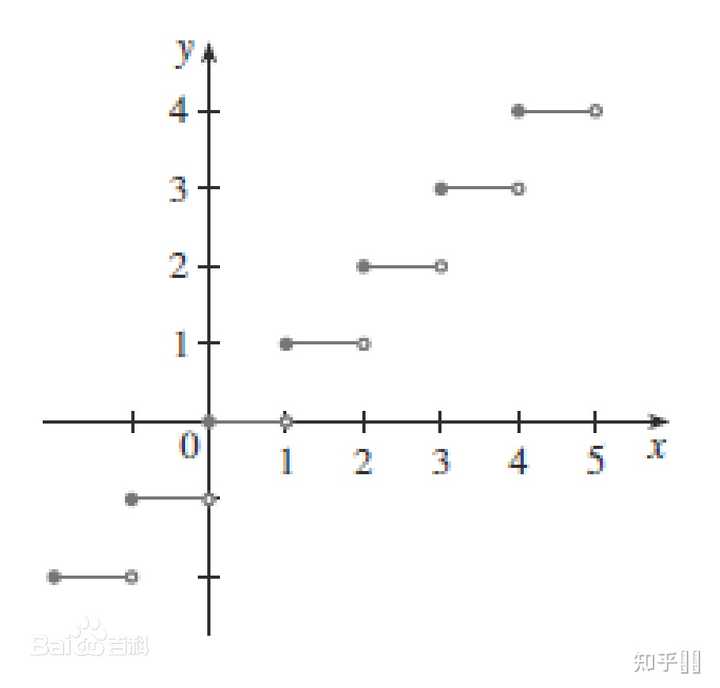
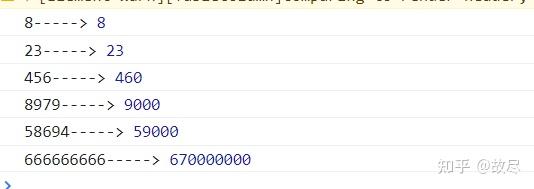
向上取整，即将一个数向上舍入到最接近的整数。比如，数字3.7和3.9都会被向上取整为4。与四舍五入不同，向上取整始终将数字舍入到更大的整数。

二、向上取整的公式

在计算机编程中，向上取整的公式通常用“ceil”或“roundup”等函数表示。然而，我们也可以使用简单的数学公式来描述这一概念。

对于任意实数x，其向上取整的公式可以表示为：

[x] = x + ⌊x⌋ - ⌈-x⌉ 

其中[x]代表x的向上取整结果，[ ]是向内取整符号，即不包含端点，比如：[x] ≥ x 的最小整数。 ⌊x⌋和 ⌈-x⌉分别是向下取整和上确界符号的代表。对于这种类型的工作我们可以借助于代码语言去计算得到一个更加明确的结果。

三、向上取整的实际应用



在数值计算中，向上取整常常用于计算面积、体积等物理量的测量值。例如，在计算材料用量时，我们通常需要使用向上取整来确保有足够的材料供应。



在金融领域，向上取整也经常被使用。例如，在计算股票交易的手续费时，由于手续费通常以整数计算，因此我们需要将交易金额进行向上取整处理。



在计算机编程中，向上取整的函数常用于控制循环次数、分配内存等任务。通过使用这些函数，我们可以更精确地控制程序的执行过程。



总之，向上取整是数学和计算机科学中常用的一个概念。通过使用相应的公式和函数，我们可以轻松地将一个数进行向上舍入操作，并将其应用于实际生活和科学研究中的各种场景中。