一、文章标题：整数集是什么


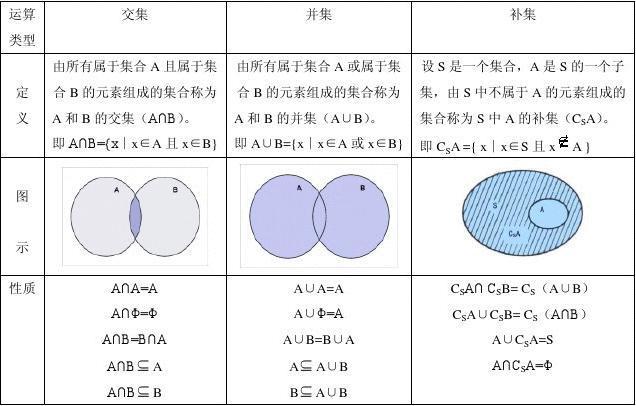
二、文章内容


整数集是一个在数学领域里常用的概念，其概念广泛地涉及到数学的各个分支，如数论、代数、几何等。下面，我们将从整数的定义开始，逐步解析整数集的内涵。

1. 整数的定义

整数，顾名思义，是数学中一个基本概念。它包括正整数、负整数和零。正整数如1、2、3等，负整数如-1、-2、-3等，而零既不是正数也不是负数。它们构成了一个集合，即整数集。

2. 整数集的表示方法

在数学中，我们常常用字母Z来代表整数集。这是因为Z的英文单词为"Zahlen"，在德语中表示“数”的意思。这样，我们就可以方便地用Z来表示所有整数的集合。

3. 整数集的性质

（1）可数性：整数集是可数的，即其元素可以按照一定的顺序一一列出，如1、2、3……等等。这种可数性使得我们能够方便地对整数集进行各种数学操作。

（2）封闭性：在整数集中进行加法或乘法运算得到的结果仍然是整数集中的元素。也就是说，整数集对加法和乘法运算封闭。

（3）有序性：整数集具有明确的顺序关系，即存在“大于”、“小于”等关系。这种有序性使得我们可以对整数进行大小比较和排序。

4. 整数集的应用

整数集在数学中有着广泛的应用。例如，在数论中，我们经常使用整数集来研究整数的性质和规律；在代数中，整数集是许多数学对象的基础，如多项式、矩阵等；在几何中，整数的性质也被用来解决一些几何问题。此外，在计算机科学中，整数集也扮演着重要的角色，如计算机程序中的计数、排序等操作都离不开对整数集的运用。

总之，整数集是数学中的一个重要概念，它具有丰富的内涵和广泛的应用。通过了解整数集的定义、表示方法和性质，我们可以更好地理解数学中的许多基本概念和原理，为进一步学习数学打下坚实的基础。