卷积的定义
在信号处理和图像处理等领域中，卷积是一个非常常见和重要的概念。下面我们就来深入探讨一下卷积的定义。


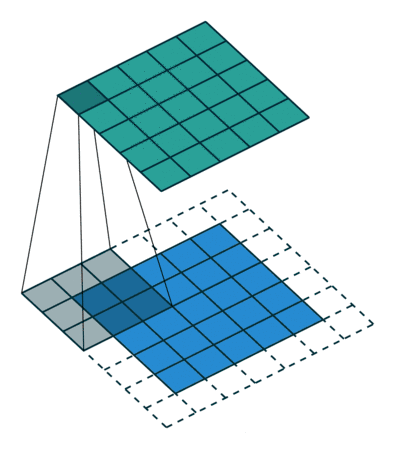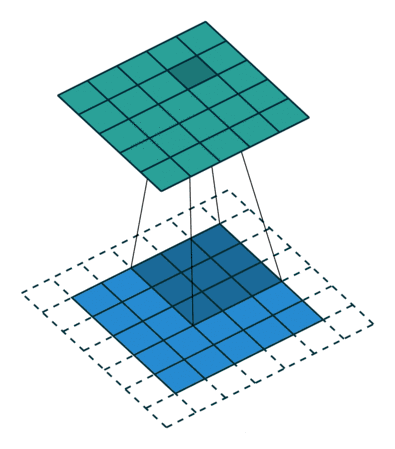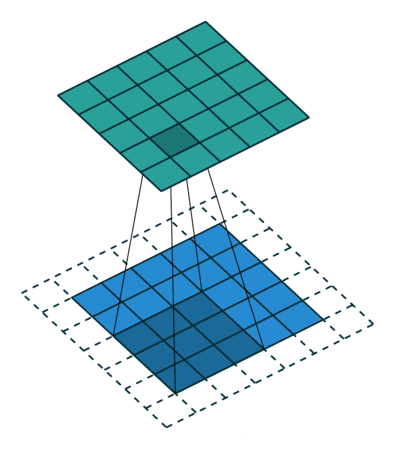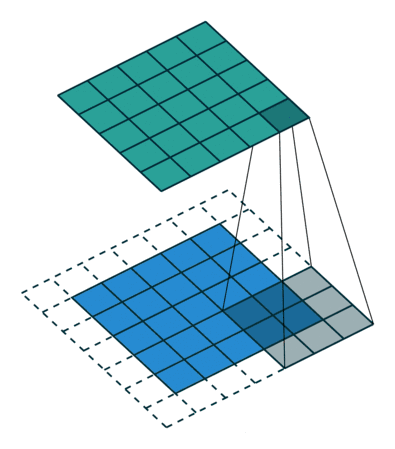
一、卷积的基本概念
卷积是一种数学运算，通常用于处理两个函数之间的相互作用。在信号处理中，我们常常将一个信号与另一个函数（称为核或滤波器）进行卷积运算，以得到一个新的信号。这个新的信号能够反映原始信号与核的某种"融合"效果。


二、卷积的数学定义
假设我们有两个函数f(x)和g(x)，那么f(x)和g(x)的卷积可以表示为f(x)与g(x)的反褶与位移的和在所有这些操作下所得函数的总和。更正式地，一维函数的卷积可以通过积分来表示：

（f*g）(n)=∫f(t)g(n-t)dt

其中*表示卷积操作，n是离散变量，∫表示积分（在离散情况下可以看作求和）。通过这个公式，我们可以看到卷积实质上是将一个函数（我们称其为核）进行反转并移动，然后将它与另一个函数进行相乘并将这些相乘结果求和。

三、卷积的应用场景
卷积在信号处理、图像处理、以及机器学习等领域都有着广泛的应用。例如，在图像处理中，我们可以使用不同的核（滤波器）进行图像的模糊、锐化、边缘检测等操作。在机器学习中，卷积神经网络（CNN）更是利用了卷积的特性进行特征的提取。

四、结论
以上就是关于卷积的定义以及其在各个领域中的应用。从上述分析中可以看出，卷积是一个强大的工具，它能够帮助我们理解和分析两个函数之间的相互作用关系，并且在很多实际应用中都有着重要的价值。通过掌握卷积的基本概念和性质，我们可以更好地理解和应用它，从而在各个领域中取得更好的成果。

以上内容就是关于卷积定义的中文文章，希望能够帮助到您！