文章标题
什么是拓扑结构


拓扑学是一种探讨物体或现象的空间布局和空间特性的学科。在计算机科学、物理学、数学、地理学等多个领域中，拓扑结构都有着广泛的应用。本文将介绍拓扑结构的基本概念、特点及其在各个领域的应用。


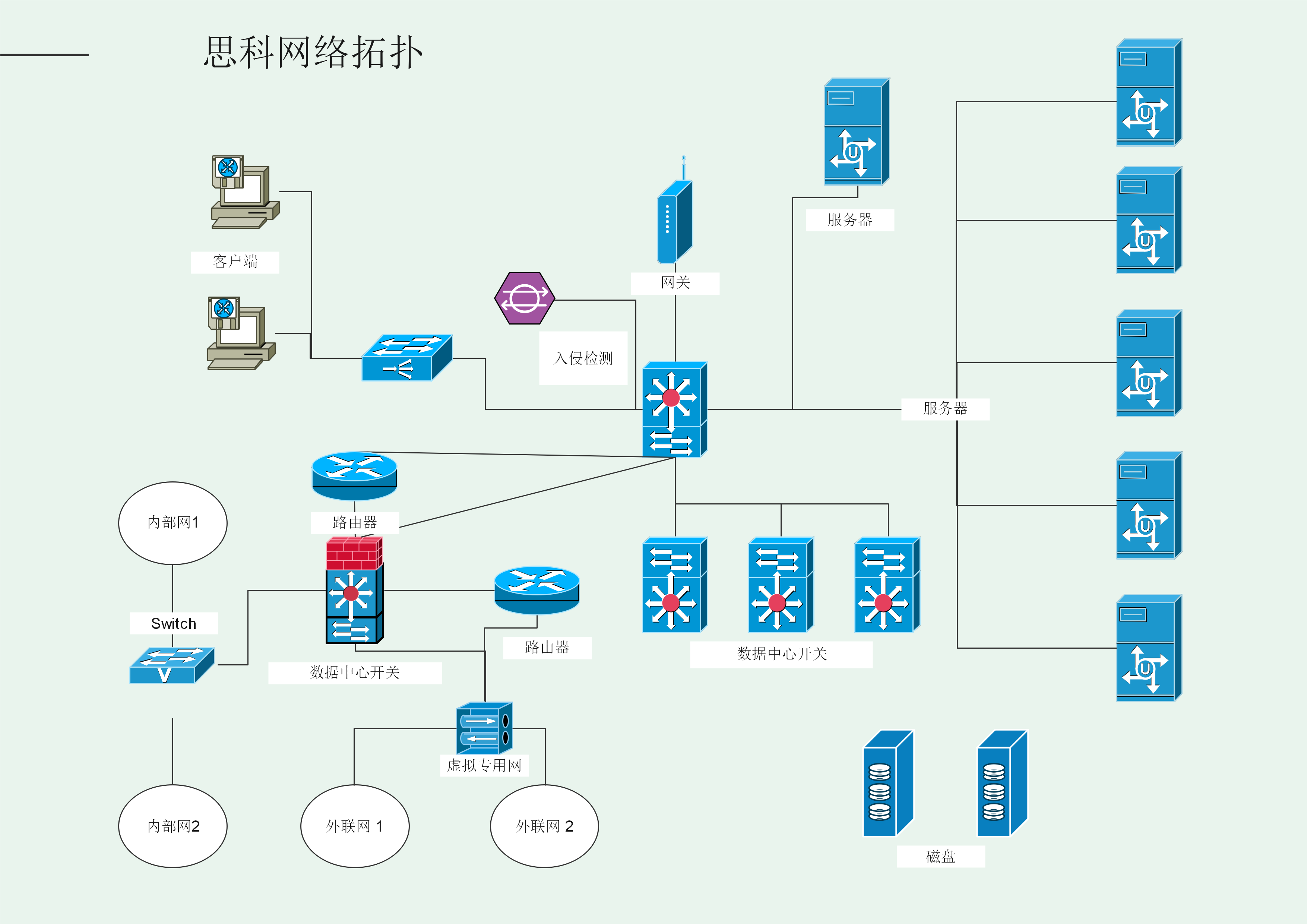
一、拓扑结构的基本概念
拓扑结构是一种抽象的数学概念，主要研究的是物体或空间中各元素之间的相对位置关系。它并不关注物体的形状、大小或细节，而是将物体视为一个连续的空间或图形，通过观察这个空间或图形的点、线、面等元素之间的连接关系来研究其特性。

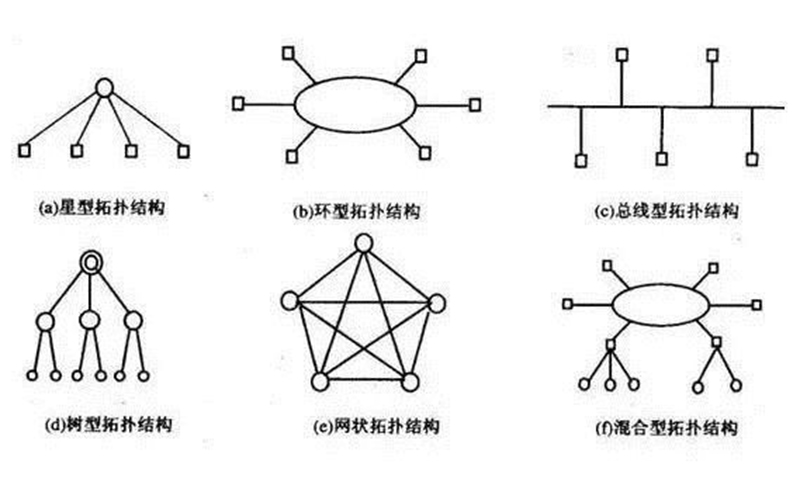
二、拓扑结构的特点
拓扑结构具有以下特点：


连续性：拓扑结构是连续的，即在任何尺度下都不会发生突然的断裂或改变。这种连续性保证了物体或空间在变换形态时保持其原有的特性。
连通性：拓扑结构中的元素之间存在某种程度的连通性，即从一个元素可以经过一系列的连续变化到达另一个元素。这种连通性决定了物体的可达性和流动性。
不变性：拓扑结构不随坐标系的改变而改变，即在不同坐标系下观察，其拓扑结构仍然保持不变。

三、拓扑结构的应用
拓扑结构在计算机科学、物理学、数学、地理学等多个领域都有着广泛的应用。例如，在计算机网络中，拓扑结构描述了网络中各个节点之间的连接关系；在地理学中，拓扑结构可以用来描述地形地貌的形态特征；在数学中，拓扑学为研究几何对象的形状和空间关系提供了有力的工具。

四、总结
拓扑结构是一种研究物体或现象的空间布局和空间特性的重要方法。它通过观察物体或空间的点、线、面等元素之间的连接关系来研究其特性，具有连续性、连通性和不变性等特点。在计算机科学、物理学、数学、地理学等多个领域中，拓扑结构都有着广泛的应用，对于深入理解和研究物体的特性和行为具有重要的意义。