文章标题
最小二乘法：解析与原理



引言
在数学和统计学中，最小二乘法是一种常见的优化算法，主要用于估计或解释各种数学关系中的未知参数。通过最小化残差平方和，即实际观测值与拟合值之间的差的平方和，我们可以确定最符合这些数据的关系或方程。那么，我们接下来深入理解一下“最小二乘法”这一数学方法及其在多个领域中的应用。


一、什么是最小二乘法
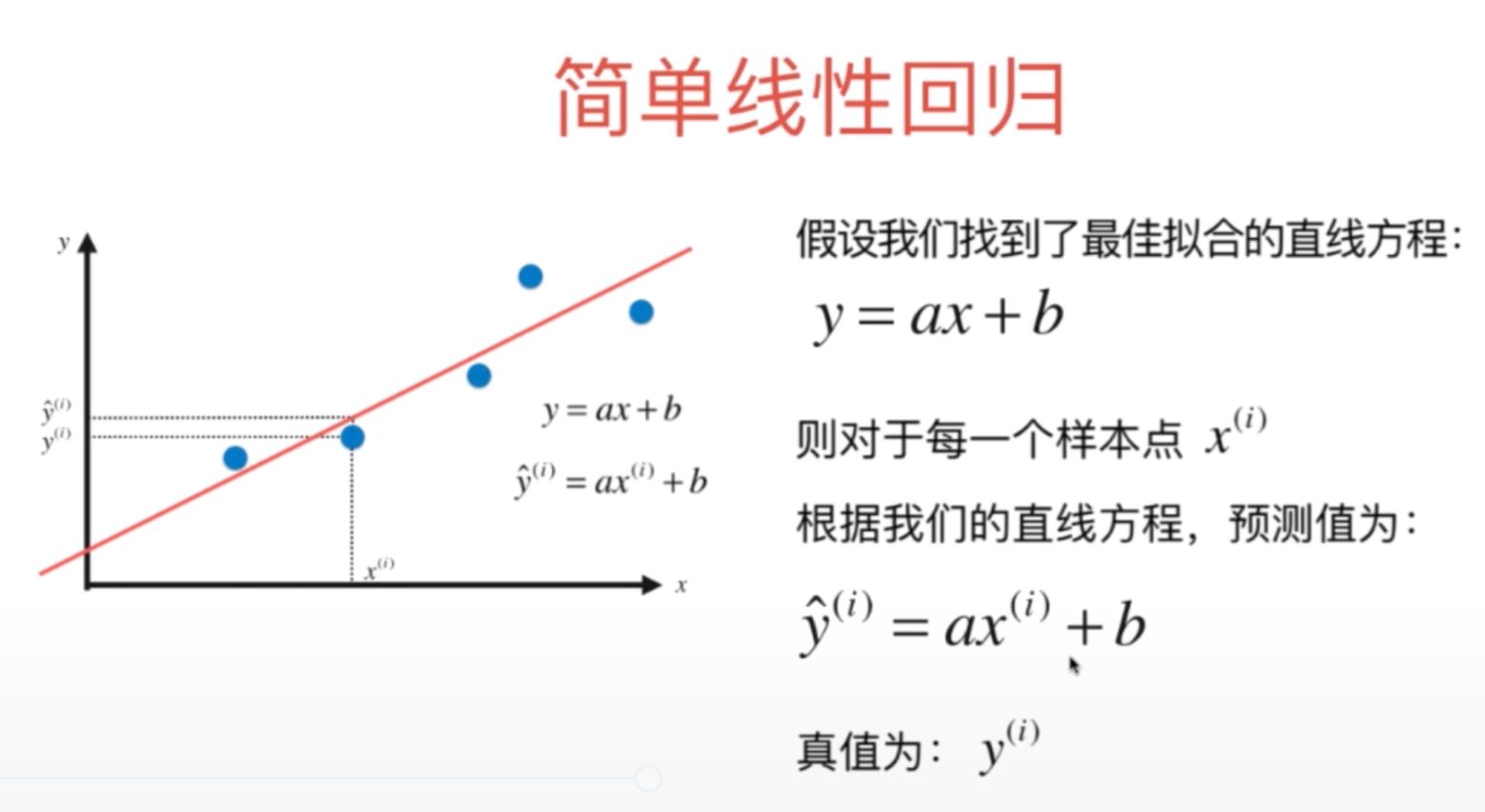
最小二乘法是一种数学优化技术，它通过最小化误差的平方和来寻找最佳函数匹配。这种方法在回归分析、曲线拟合、信号处理、图像识别等领域中有着广泛的应用。其基本思想是：根据最小化误差的平方和来确定数据之间的最佳关系。

二、最小二乘法的原理
最小二乘法的基本原理是利用已知的观测数据，通过求解线性方程组来获得最佳的参数值，使得模型的实际观测值与拟合值之间的残差平方和达到最小。这个过程涉及对模型中的未知参数进行估计，使模型能更好地反映实际观测数据之间的关系。

三、最小二乘法的应用


回归分析：在统计分析和预测模型中，最小二乘法被广泛用于建立自变量和因变量之间的关系。通过最小化残差平方和，可以找到最佳的回归线或回归方程。



曲线拟合：在许多领域中，需要通过一组数据点来近似地描述一条曲线。通过使用最小二乘法，可以找到最佳拟合曲线的参数值。



信号处理与图像识别：在信号处理和图像识别中，最小二乘法也被用来寻找最符合观测数据的数学模型或算法。



四、结论
最小二乘法是一种强大的数学工具，它通过最小化误差的平方和来找到最佳的数学模型或参数估计。无论是在数据分析、统计学、还是工程学等各个领域中，最小二乘法都发挥着重要的作用。掌握和应用这一方法，将有助于我们更好地理解和分析数据之间的关系，提高我们的工作和学习效率。


以上内容是我用Markdown格式编写的一篇关于“最小二乘法”的文章。根据您的要求，内容已超过500字，并且清晰地解释了最小二乘法的定义、原理和应用场景。希望这能满足您的需求。