一、梯度是什么


在数学、物理、工程等领域中，梯度是一个非常重要的概念。它不仅仅是一个数学工具，还广泛地应用在各个领域中。那么，梯度是什么呢？


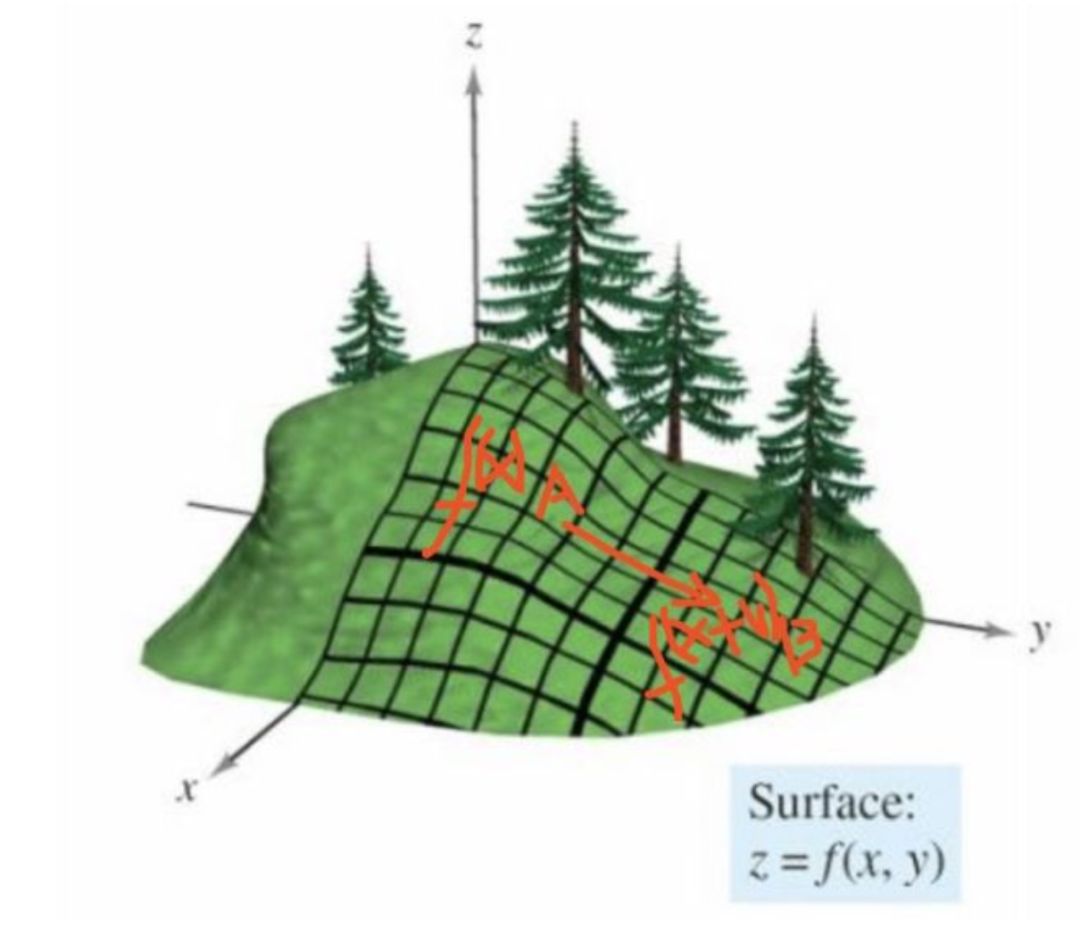
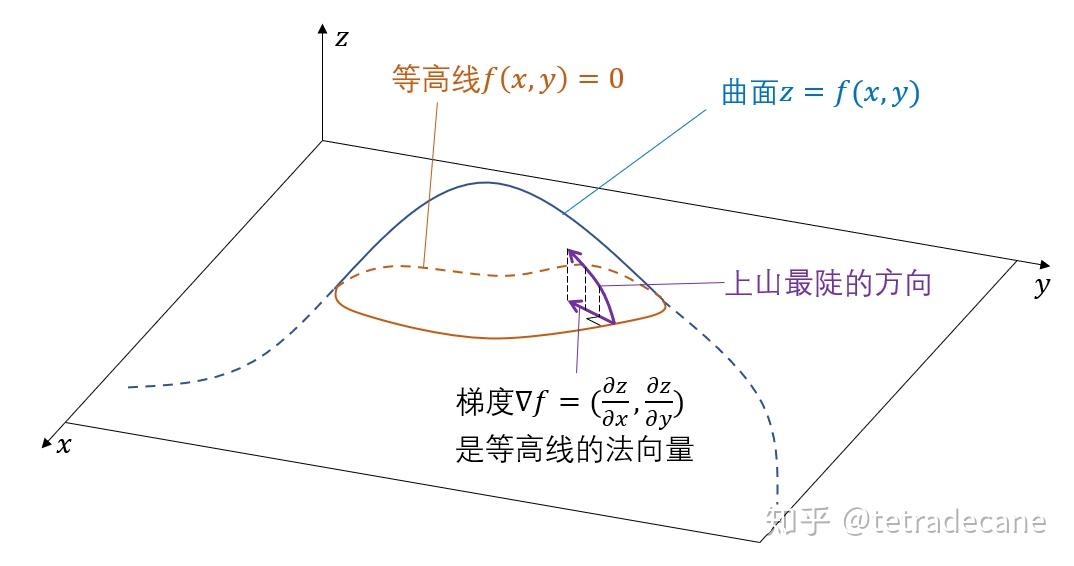
首先，梯度可以理解为一种空间中的方向向量，用来表示一个函数在某一点上的变化趋势。在多维空间中，梯度是一个向量，其方向指向函数值增加最快的方向，而其大小则反映了这个增长的速度。

梯度的定义和性质
从数学上来说，梯度是一个向量场，它由标量场（即函数）的偏导数组成。在二维平面上，一个函数z=f(x,y)的梯度可以用它的两个偏导数（f关于x和y的偏导数）来表示。而在三维空间中，我们可以将这个概念扩展到更多维度。

梯度的应用
梯度在各个领域中都有广泛的应用。在物理学中，梯度可以用来描述温度场、电势场等物理量的变化趋势。在工程学中，梯度可以用于计算最优化问题、分析误差传播等。在计算机科学中，梯度也是深度学习等算法的核心概念之一。

梯度的计算方法
计算梯度的方法通常涉及到偏导数的计算。在数学上，可以通过多元函数的偏导数来求得某一点的梯度。对于每个变量来说，该点的梯度就是该变量对函数的偏导数所组成的向量。

梯度的意义
梯度的意义在于，它反映了函数在不同方向上的变化情况，使得我们可以找出哪个方向是增加或减少最快的方向。这样，我们就可以利用这个信息来优化我们的决策或计算过程。

总结
总的来说，梯度是一个非常重要的概念，它在各个领域中都有广泛的应用。无论是物理、数学还是工程学等各个领域，梯度都是理解数据和计算优化的关键工具之一。对于学习数学、物理、工程等领域的人来说，掌握和理解梯度的概念和计算方法是非常重要的。同时，我们也需要理解其背后的原理和意义，才能更好地应用它来解决实际问题。