二进制加法运算
主机域名文章
2025-01-10 08:50
370
标题:二进制加法运算
在我们学习计算机的基本知识时,常常会接触到一种称为二进制的数制。它是计算机内部储存和处理数据的一种重要形式。理解二进制的基础,当然包括掌握其加法运算。
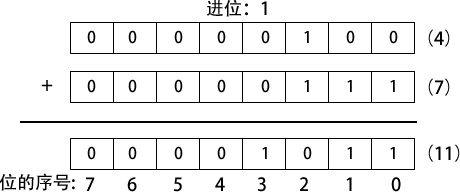
一、什么是二进制

二进制是一种以2为基数的计数系统,采用0和1两种符号来表示数值。它常被用于计算机中,因为二进制数的抗干扰能力强、可靠性高、因为每位数据只有高低(即二进制的1或0)两个状态,不像十进制需要依靠外部信号大小(即多个单位位的组合)。
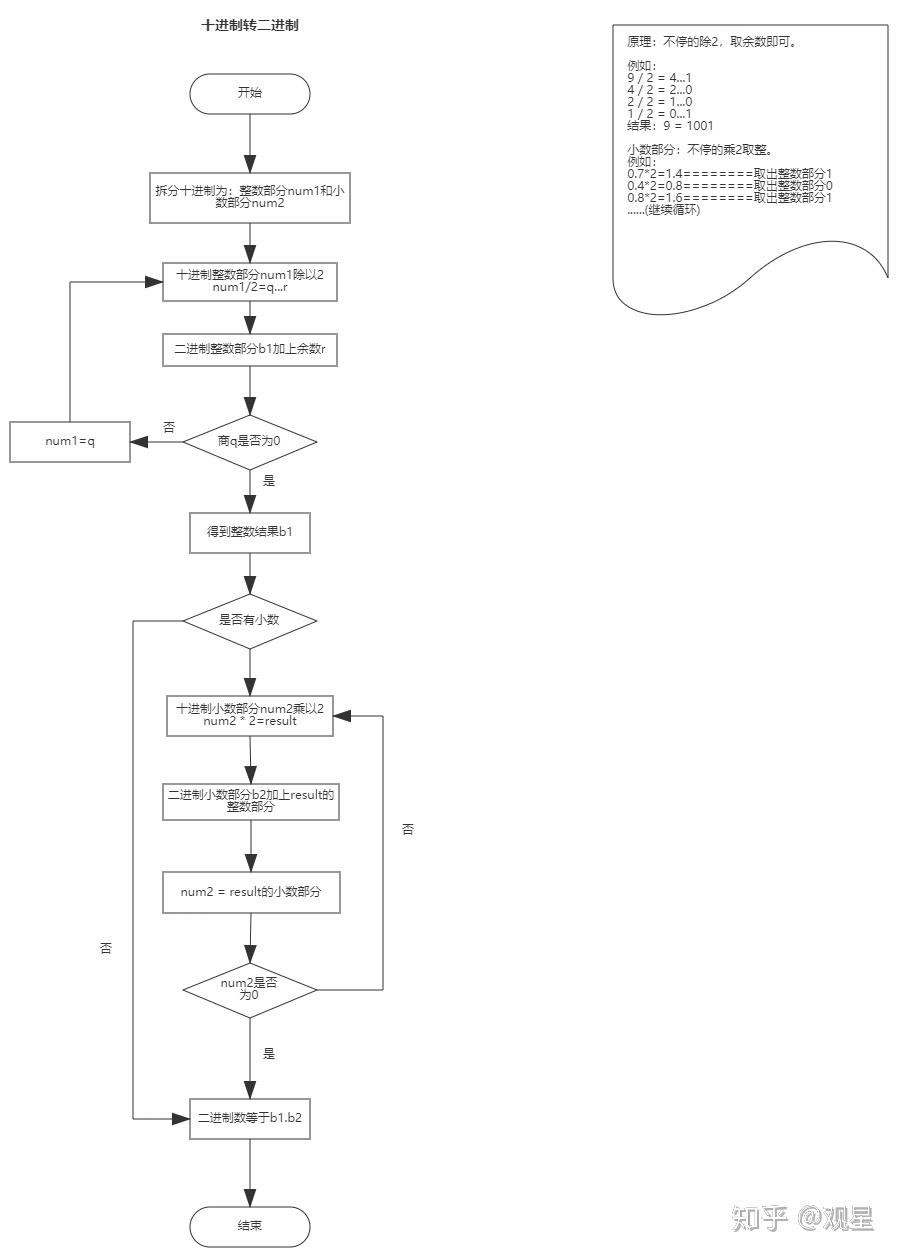
二、二进制加法原理
在二进制中,我们主要采用"逢二进一"的原理进行加法运算。和十进制相似,但我们使用的是一个基础的“位值系统”,每个位置代表的权重都是2的倍数。因此,我们需要了解在每一个位置上的二进制数加权是多少,然后再按照二进制加法规则进行运算。
三、具体步骤
二进制加法操作与十进制加法有些许不同,以下是具体步骤:
- 对齐位数:先确定两个二进制数中位数最多的位数,然后其他数位对齐。
- 逐位相加:从最低位(右起第一位)开始,逐位相加,如果相加结果为1,则向高位(左位)进位;如果相加结果为2,则向高位进位并本位变为0。
- 考虑进位:每次相加时,都需要考虑上一位是否有进位,然后决定本位的数值。
- 最终结果:最后得出的就是计算的结果。如果最高位有进位则继续向高位进位,直到没有进位为止。
四、例子说明
以“1011”(二进制)和“100”(二进制)相加为例:
- 从右向左依次计算各位数(因为低位影响更大),首先是两个数字的最右边的两个单位:1 + 0 = 1 (剩余没有进位) + 0 + 1(本位的进位) = 1 (继续保留) ,继续向前进行相同操作直到算完。最终结果是 “1010” (由于末尾的2没有前一位接收,就进到了高位),而最后的高位如果有进位需要继续算到更前面去。
通过以上的解释和例子,我们可以发现,二进制加法其实与十进制有许多相似之处,只是它使用的是二进制的规则而已。理解并掌握好这个规则,对于我们理解计算机的内部工作原理有着重要的意义。希望这篇文章能帮助你更好地理解二进制的加法运算。
标签:
- 关键词:二进制
- 加法运算
- 位值系统
- 进位
- 二进制数
- 十进制
- 计算机内部工作原理

