单变量求解
主机域名文章
单变量求解
2024-12-31 12:30
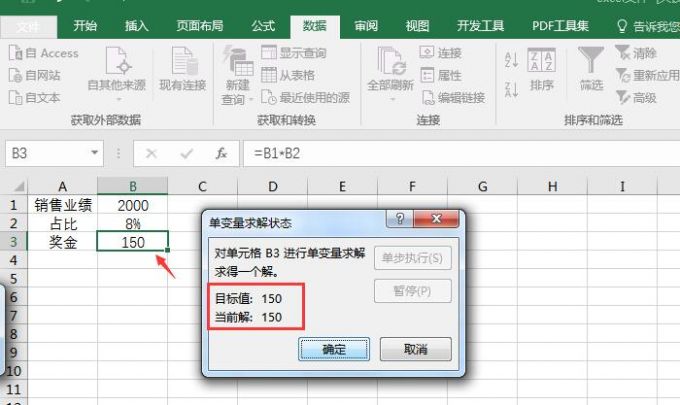
单变量求解:用于解一个未知数问题的算法,涵盖移项、合并同类项、乘除法和开平方等方法。
一、文章标题
单变量求解:原理、方法与实例
二、文章内容
在数学和计算机科学中,单变量求解是一种常见且重要的算法。它通常用于解决只有一个未知数的数学问题,如方程求解、函数值计算等。本文将介绍单变量求解的原理、方法及实例。
一、单变量求解的原理
单变量求解的核心思想是,给定一系列的已知条件(例如已知量与未知数之间的关系式),利用某种方法确定未知数的具体数值。这一过程涉及基本的代数原理,包括方程式和表达式。单变量求解的目标是将一个复杂或多个未知数的表达式简化到一个单一的未知数,然后解出该未知数的具体值。
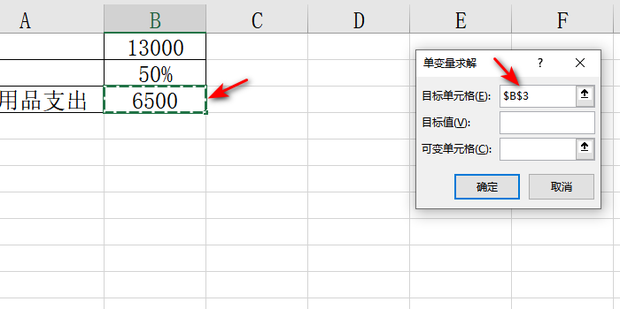
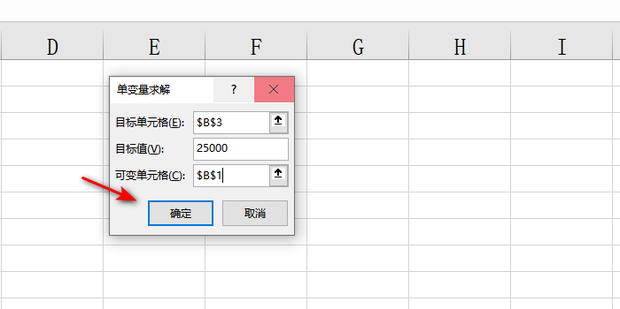
二、单变量求解的方法
- 移项法:将方程式中的已知量移到等式的一边,未知量移到另一边,然后进行化简和计算。
- 合并同类项法:将方程式中相同未知数的项合并在一起,便于求解。
- 乘除法:利用已知量对等式进行乘除操作,消除分母或将复杂的方程式化简为更简单的形式。
- 平方根法:通过开平方来解方程中的未知数。
- 公式法:根据已知条件列出相关的公式,直接求出未知量的值。
三、单变量求解的实例
例如,我们有一个简单的线性方程 x + 3 = 8,我们可以利用移项法求解:
首先,将3移到等式的右边,得到 x = 8 - 3。
然后进行计算,得到 x = 5。
这就是我们的答案,即未知数x的值为5。
再如,我们要求解一个二次方程的根,如 ax^2 + bx + c = 0。这时我们可以使用公式法来求解:x = [-b ± sqrt(b^2 - 4ac)] / 2a。通过这个公式,我们可以轻松地求出二次方程的根。
以上就是单变量求解的基本原理、方法和实例介绍。通过这些内容,我们可以看到单变量求解在数学和计算机科学中的应用广泛,掌握它有助于我们更好地理解和解决各种实际问题。同时,也让我们了解到算法和计算机程序中的逻辑思维是如何形成的,为我们学习其他复杂的算法和技术打下了坚实的基础。
标签:
- 单变量求解
- 原理
- 方法
- 实例
- 数学问题
- 计算机科学
