文章标题：STDEV 详解
在统计与数据分析领域中，STDEV 是一个常见的概念。它通常指代样本的标准差（Standard Deviation）的缩写。接下来，我们将深入探讨 STDEV 的概念、计算方法以及它在数据分析和统计中的应用。


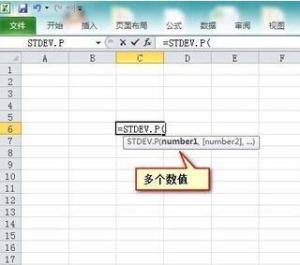
一、STDEV 的概念
标准差是用于衡量数据集中数据分布散度的度量标准。当我们讨论数据的集中程度和波动性时，标准差是一种非常重要的指标。一个较小的标准差表示数据集接近其平均值，而较大的标准差则表示数据分布更加分散。


二、STDEV 的计算方法
STDEV 的计算主要依赖于数据集的均值和平方差。计算过程分为以下几个步骤：


计算数据集中所有数值的均值（算术平均数）。
对每个数值，计算其与均值的差值（即偏差）。
将这些偏差平方后相加，得到平方和。
将平方和除以数据的数量（N-1），即样本数量减去一（通常称为“n”），得到方差。
对方差取平方根，即为标准差（STDEV）。

三、STDEV 在数据分析中的应用
1. 识别数据的正常分布情况
如果数据集中每个值都与均值差距较大，说明数据的离散程度高；如果所有数据与均值都相差不大，那么该数据集更接近正态分布。这有助于我们更好地理解数据的分布情况。

2. 判断数据集的稳定性
标准差可以作为衡量数据集稳定性的一个指标。在考虑进行不同操作或应用不同分析时，比如加入新的元素或引入某些参数变动，了解STDEV的值能为我们提供更好的判断依据。当发现 STDEV 有所波动或大幅增长时，可能意味着数据集的稳定性受到威胁，需要进一步分析或调整。

3. 比较不同数据集的离散程度
当需要比较不同数据集的离散程度时，STDEV 可以作为衡量工具之一。较高的 STDEV 可能表示数据点分散得更加广泛，而较低的 STDEV 则表明数据更接近平均水平。这种信息在评估多组实验结果或处理各种市场或金融指标时尤其有用。

总之，STDEV 在统计和数据分析中扮演着重要角色。它不仅能帮助我们了解数据的分布情况，还能评估数据的稳定性和离散程度。通过掌握 STDEV 的概念和计算方法，我们可以更好地利用这一工具来分析数据、做出决策并解决实际问题。