Markdown格式排版文章：



文章标题：数学中的e

一、引言
在数学中，e是一个非常重要的常数，它常常出现在各种复杂的数学公式和计算中。虽然e的初始定义可能看起来有些复杂，但它在许多领域都有广泛的应用。本文将详细介绍e的起源、定义、性质以及应用。


二、e的起源和定义
e最初是由数学家约翰·纳皮尔斯在16世纪发明的，当时他试图寻找一个表示连续复利增长的数值。后来，欧拉将其命名为“自然对数的底数”，并为其赋予了“e”这个符号。

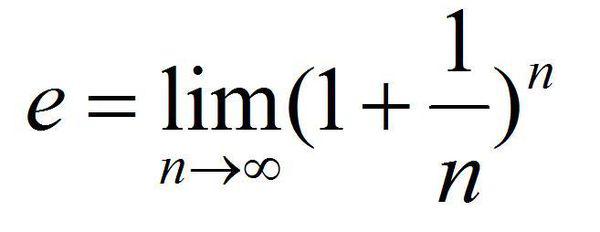
e的定义是：e是自然对数的底数，即满足e的指数函数等于其自身微分函数的数。具体来说，如果y=ex，那么y的导数就是y自身，这是微积分中的一个基本公式。

三、e的性质
e具有许多独特的性质。首先，它是无理数，无法用简单的分数或整数表示。其次，它的值非常接近于2.71828，且是一个超越数。这些特性使得e在数学和其他领域有着广泛的应用。

此外，e在微积分、概率论和统计中扮演着重要角色。在微积分中，e经常出现在各种公式和定理中，如泰勒级数展开式等。在概率论和统计中，e常用于描述随机变量的分布和变化规律。

四、e的应用
e在许多领域都有广泛的应用。在金融学中，连续复利的计算就涉及到e的使用。此外，在生物学、物理学、计算机科学等领域也经常使用到e。例如，在计算机科学中，e被用于描述计算机程序的运行时间和资源消耗等指标。

总之，e是一个非常重要的数学常数，它在数学和其他领域都有着广泛的应用。通过了解e的起源、定义、性质和应用，我们可以更好地理解其在科学研究和实际应用中的重要性。

五、结论
本文介绍了数学中的常数e的起源、定义、性质和应用。通过了解这些内容，我们可以更好地理解e在数学和其他领域的重要性。虽然e的初始定义可能有些复杂，但它在各种复杂计算和公式中扮演着不可或缺的角色。因此，我们应该更加重视对e的学习和研究，以便更好地应用它于实际生活和工作中。


希望这篇文章能满足您的需求！如果还有其他问题或需要进一步帮助，请随时告诉我。