一、阶乘函数


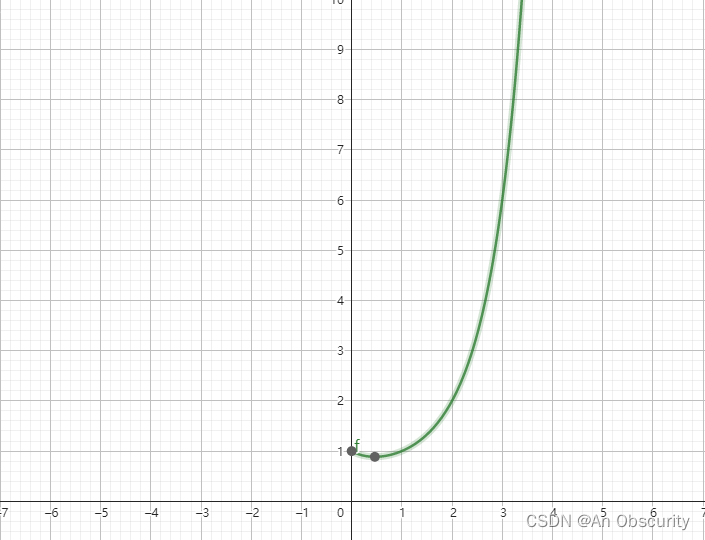
阶乘函数是数学中一个非常重要的概念，尤其在组合数学和计算机科学中有着广泛的应用。接下来我们将从定义、性质和实际应用等方面对阶乘函数进行探讨。


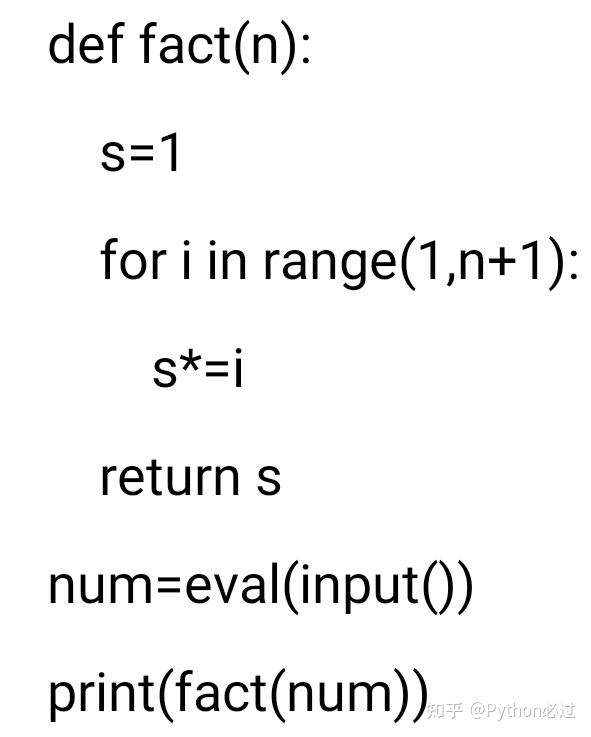
一、定义

阶乘函数是一种在数学中经常用到的数学函数，用记号n!表示，即n的阶乘（factorial）。具体定义为从1开始，递乘到n的所有正整数的乘积。例如，5! = 5×4×3×2×1=120。

二、性质

阶乘函数具有以下基本性质：


阶乘函数的值总是正整数，且随着n的增大，其值迅速增长。
阶乘函数具有很好的代数性质，如乘法法则：n! = n × (n-1)!。
阶乘函数与排列和组合密切相关，常用于计算排列数和组合数。

三、实际应用

阶乘函数在数学、物理、计算机科学等领域有着广泛的应用。以下是一些具体的应用场景：


排列和组合：阶乘函数常用于计算排列数和组合数。例如，从n个不同元素中取出r个元素的所有排列的个数为n的阶乘除以(n-r)!。
概率论：在概率论中，阶乘函数常用于计算事件的排列和组合情况，从而得到事件的概率。
计算机科学：在计算机科学中，阶乘函数常用于算法的时间复杂度和空间复杂度的分析。
物理科学：在物理科学中，阶乘函数也被广泛用于量子力学和粒子物理的描述。例如，计算能级、动量分布等问题常常会用到阶乘函数。

总之，阶乘函数是数学中的一个重要概念，其简洁而有力的表达方式使其在众多领域有着广泛的应用。对于理解和掌握这一基本概念，不仅需要掌握其定义和性质，还需要在实际应用中加以运用和实践。只有这样，才能真正掌握这一强大而富有实用性的数学工具。