Markdown格式的标题与高质量中文文章
文章标题
浮点：概念与原理


一、浮点概念
在计算机中，浮点是指以特定的格式存储和计算实数的一种方式。而浮点数（浮点类型数据）在计算机程序中广泛应用，尤其在数学运算和数值处理方面发挥着至关重要的作用。它拥有处理复数和精密运算等关键优势，相较于其他的数据类型更为方便灵活。


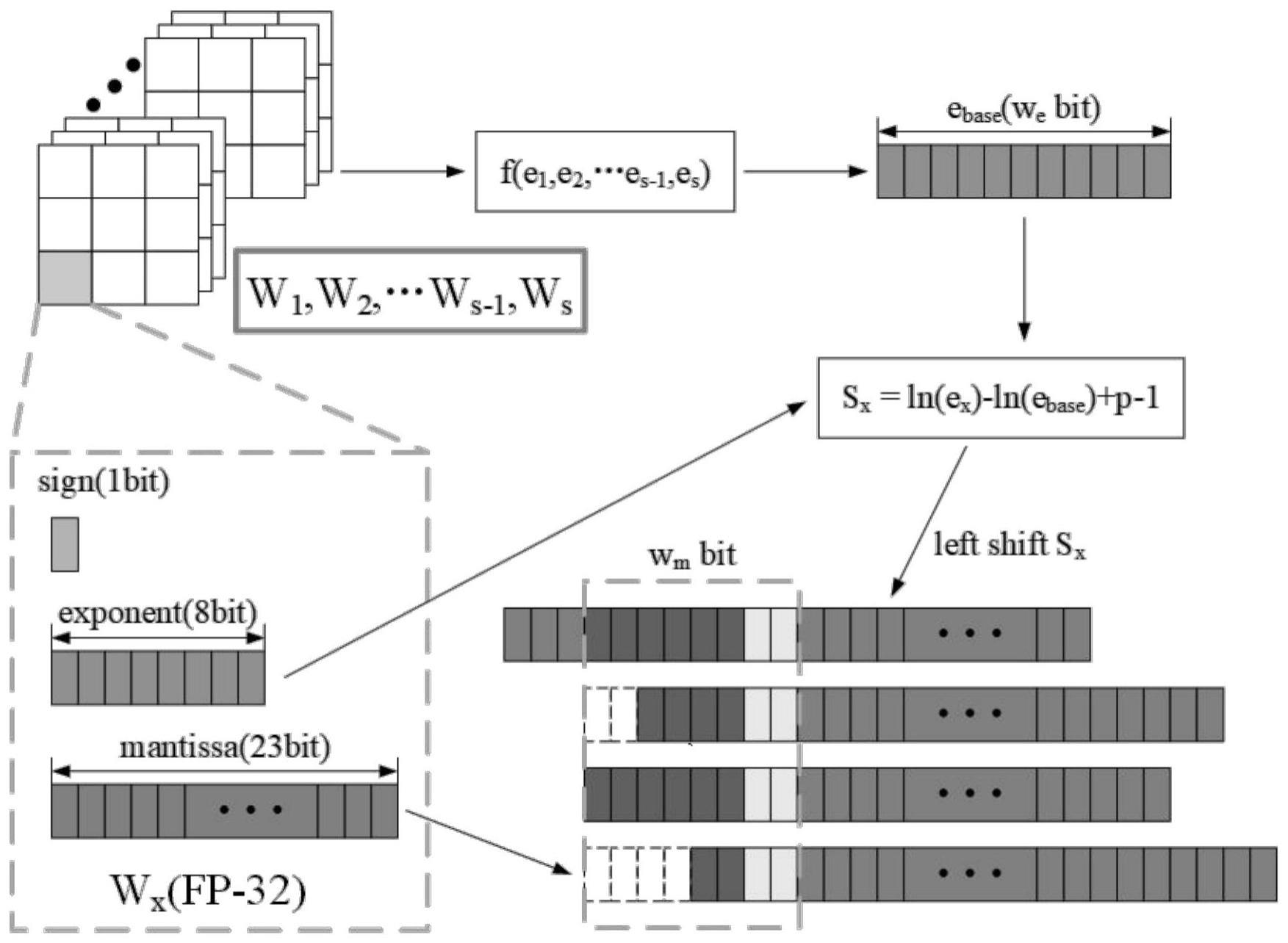
二、浮点的基本原理
在计算机科学中，每个浮点数都有符号位、指数和尾数三个部分组成。其中，符号位决定了数的正负；指数决定了数的范围大小；尾数则决定了数的精度。三者共同构成了浮点数的核心原理。

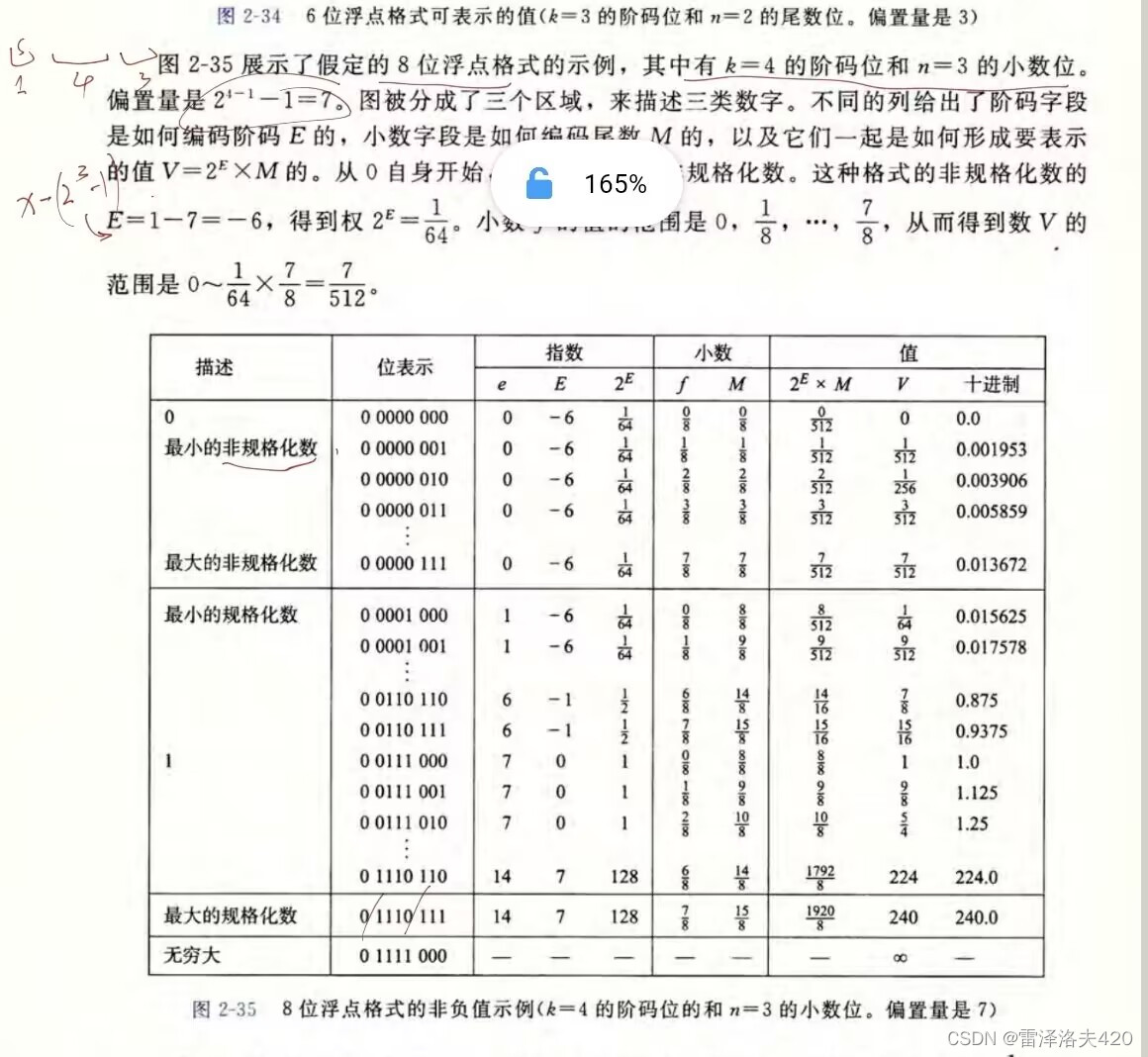
1. 符号位
符号位用来表示数的正负，通常用0表示正数，用1表示负数。这和其他有符号数字的概念一样，决定这个数的初步表达方式。

2. 指数（尾数部分）
浮点数的指数用于描述该数的大致范围。指数越大，数值越大；指数越小，数值越小。而指数的表示方式通常采用科学计数法，即用E或e表示指数部分。

3. 尾数部分
尾数决定了数值的精度，其包含了所有有效数字。通常在计算机中以二进制的形式进行存储，这就涉及到了二进制转换的问题。不同的二进制位对浮点数的精度有不同的影响。

三、总结与扩展
总的来说，浮点是计算机数值处理的关键概念，对程序员理解编程中的数值计算有着重要的意义。在计算机科学中，我们经常需要处理各种类型的数值数据，而浮点就是其中最为重要的一种类型之一。理解其原理和特性，对于编写高质量的代码和算法具有重要作用。同时，在实际编程过程中，也需要关注如何精确地进行浮点运算，以避免出现诸如舍入误差等常见问题。

四、实际应用与注意事项
在实际编程过程中，需要谨慎处理浮点运算。因为计算机中的浮点运算可能存在精度问题，这可能会影响到我们的计算结果。为了减少这种误差，我们可以采取一些措施，如使用高精度的库函数进行计算、合理选择算法和精度等。此外，在实际应用中还需要根据不同的需求和场景选择合适的浮点类型和数据结构来满足实际需求。

通过以上的讨论，我们了解了浮点的概念和基本原理，也了解了一些在应用中需要注意的问题和策略。相信对编程领域相关内容感兴趣的人在阅读后一定会有所收获和帮助。同时这也对撰写高质量的代码提供了宝贵的理论依据和操作建议。