一、弧度单位


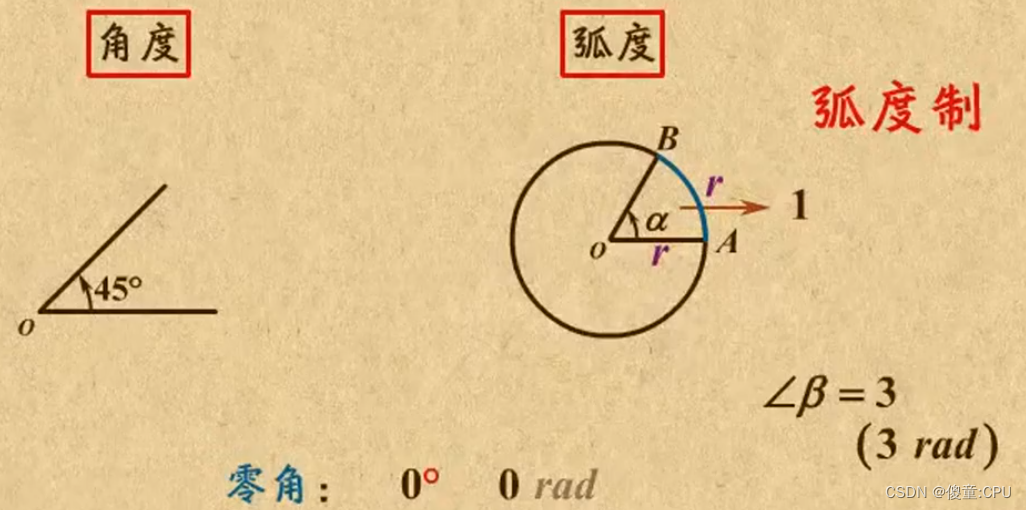
在数学和三角学中，弧度是角度的度量单位。与常见的角度制不同，弧度制以弧度数来衡量角度的大小，它是一种国际上广泛使用的角度度量标准。本文将探讨弧度单位的定义、特性以及在各个领域中的应用。


1. 弧度定义

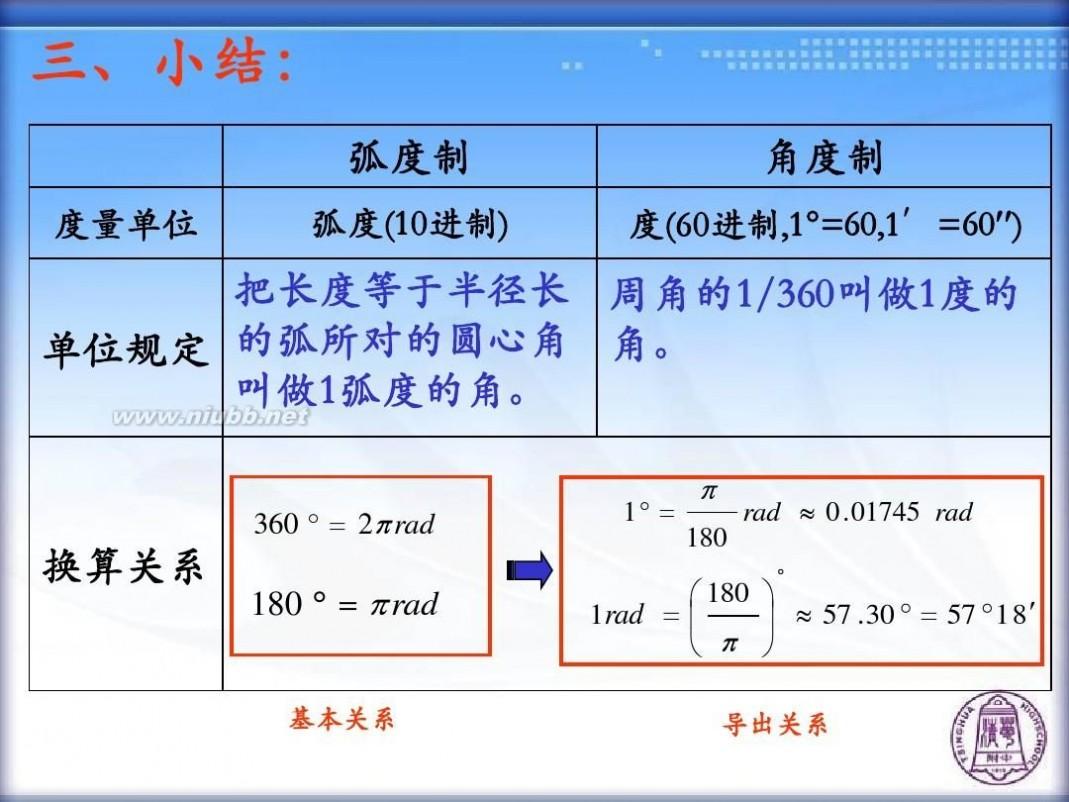
弧度，是一种量度角度的单位制度，由希腊文“radian”翻译而来。在数学中，一个完整的圆周角被定义为360度或2π弧度。因此，弧度的定义就是以圆周为基准，将圆周的任意一段弧长与半径的比值定义为该弧对应的弧度值。用数学表达式表示就是：弧度 = 弧长/半径。

2. 弧度的特性

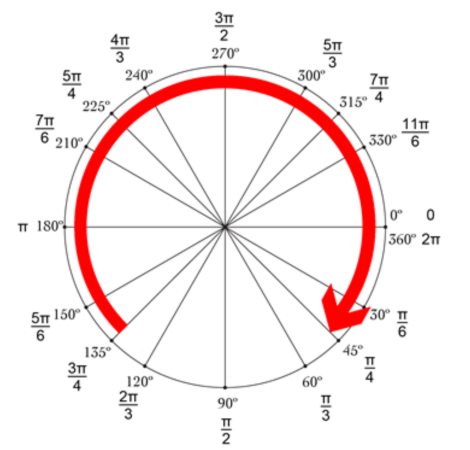
弧度与角度之间存在转换关系，并且这种转换是线性的。例如，一个完整的圆周角（即360度）等于2π弧度（约等于6.2832）。同时，弧度具有累加性，两个角的弧度值可以相加。这些特性使得弧度成为数学计算中方便使用的度量单位。

3. 弧度的应用

（1）三角函数计算：在三角函数中，常使用弧度作为角度的度量单位。这是因为使用弧度可以简化三角函数的计算过程，提高计算的精确性。

（2）几何学：在几何学中，弧度被广泛应用于计算圆的周长、面积、扇形面积等。此外，在研究曲线、曲面等复杂几何形状时，也需要用到弧度这一度量单位。

（3）物理学：在物理学中，弧度常被用于描述物理量随时间的变化率，如角速度等。同时，在描述电磁波、振动等物理现象时，也需要用到弧度这一度量单位。

（4）其他领域：除了数学和物理学，弧度还在工程学、地理学、天文学等领域有着广泛的应用。例如，在地理学中，可以用弧度来描述两个地点之间的经纬度差；在天文学中，可以用弧度来描述行星或恒星之间的角度关系等。

总之，弧度作为一种国际上广泛使用的角度度量标准，具有简单、方便、易用的特点。在各个领域中都有着广泛的应用，是现代科学研究和工程实践中不可或缺的一部分。

以上就是关于弧度单位的介绍，希望能够帮助您更好地理解这一概念及其在各个领域中的应用。