概率密度函数

一、概率密度函数

引言

概率密度函数，在数学与统计领域中扮演着举足轻重的角色。无论是自然科学还是工程学，乃至经济学，概率密度函数的应用无处不在。它为理解随机现象和其背后规律提供了重要工具。

一、概率密度函数的概念

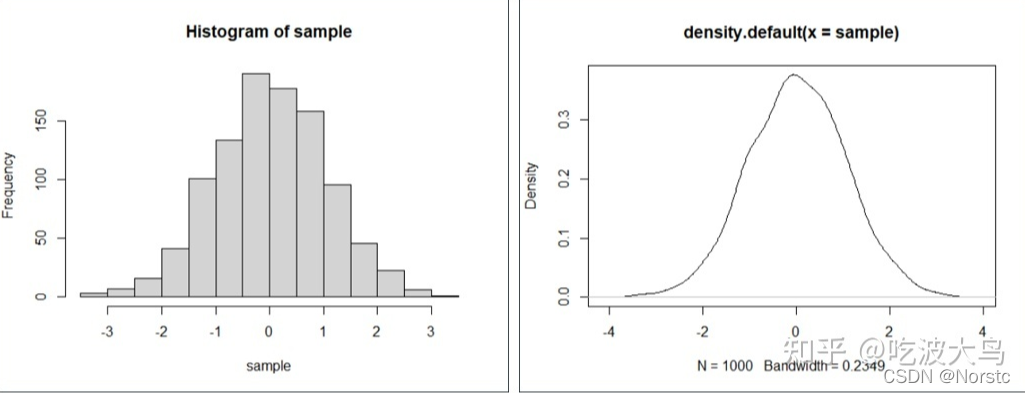
概率密度函数（Probability Density Function，简称PDF）是对随机变量的一种表示形式，具体指代连续随机变量在某一给定区间上的可能性。当涉及到的是离散随机变量时，通常使用的是概率分布函数（Discrete Distribution Function）。

二、概率密度函数的性质

1. 非负性：对于所有实数x，PDF的值都是非负的。这意味着随机变量取某一值的概率不可能为负。
2. 归一性：在实数范围内对PDF进行积分，其结果为1，即表示随机变量落在某一范围内的总概率为1。
3. 局部信息：PDF能提供关于随机变量在不同点处的可能性的具体信息。

三、常见概率密度函数

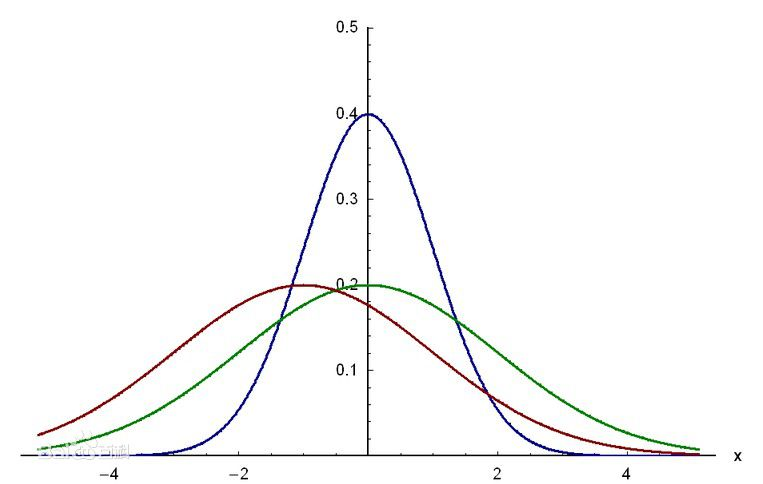
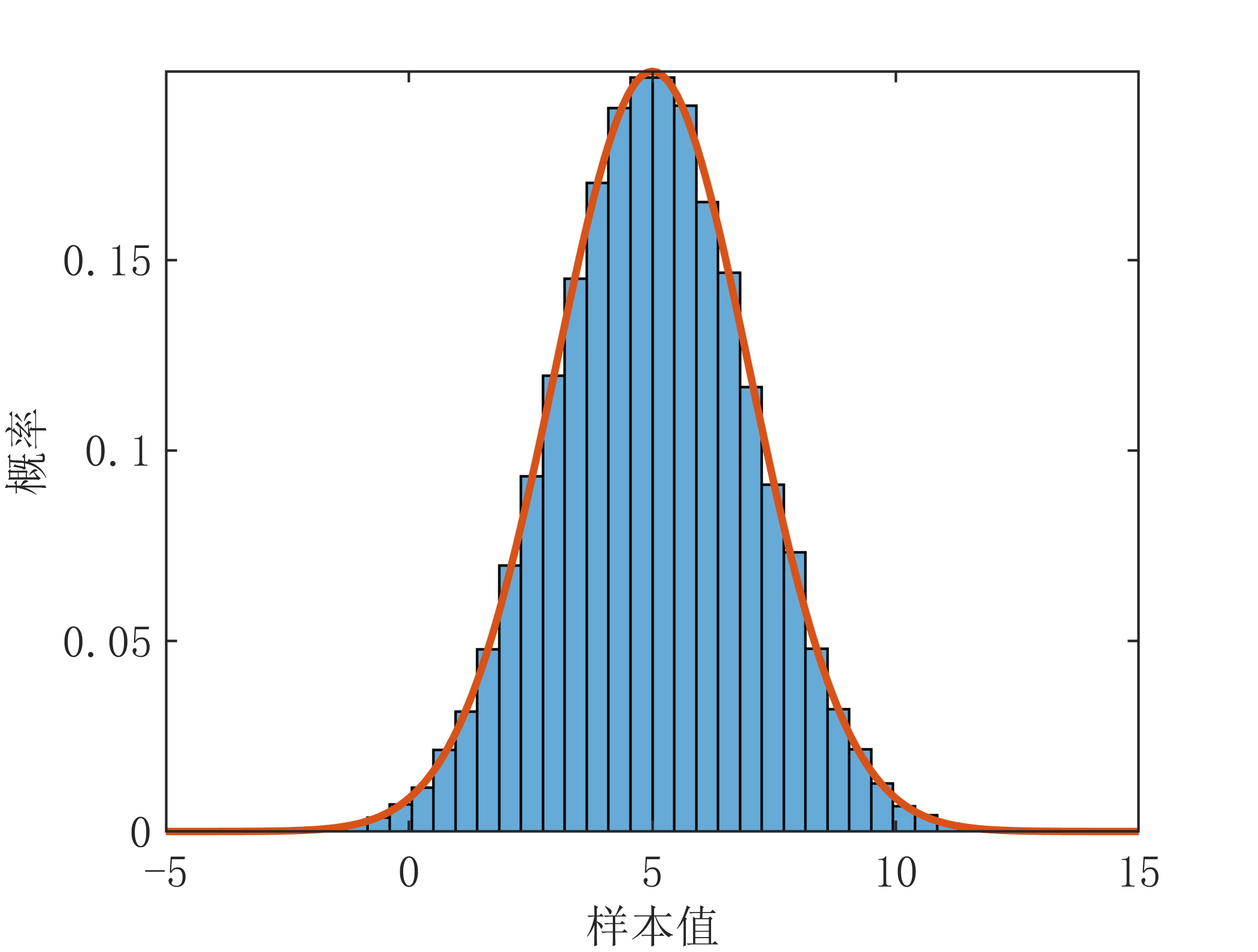
1. 正态分布（Gaussian Distribution）：在许多自然现象和许多其他领域中，正态分布的概率密度函数非常常见。它具有两个参数：均值和标准差。
2. 指数分布：常用于描述事件发生的时间间隔或某些物理量的分布情况。
3. 均匀分布：在某个特定区间内，其概率密度函数是恒定的。

四、应用场景

由于概率密度函数能够提供关于随机变量在某一特定点或区间上的可能性信息，因此它在许多领域都有广泛的应用。例如，在金融领域中，它可以用于分析股票价格或市场波动的可能性；在医学领域中，它可以用于研究疾病的发病率或死亡率等。

五、总结

概率密度函数是理解随机现象的重要工具之一。它通过提供关于随机变量在不同点或区间上的可能性信息，帮助我们更好地理解随机现象的规律和特性。同时，它也是许多其他统计方法和模型的基础，如假设检验、回归分析等。因此，掌握和理解概率密度函数对于数学和统计的学习和应用具有重要意义。

以上就是关于概率密度函数的简要介绍和解析，希望对大家有所帮助。