导数符号：解读数学的奇迹

导数在数学中，有着极为重要的地位，其不仅揭示了函数的变化速度和方向，也是各种工程学、经济学以及自然科学的重要工具。然而，要想深入理解导数的奥秘，我们需要首先掌握导数符号的使用。

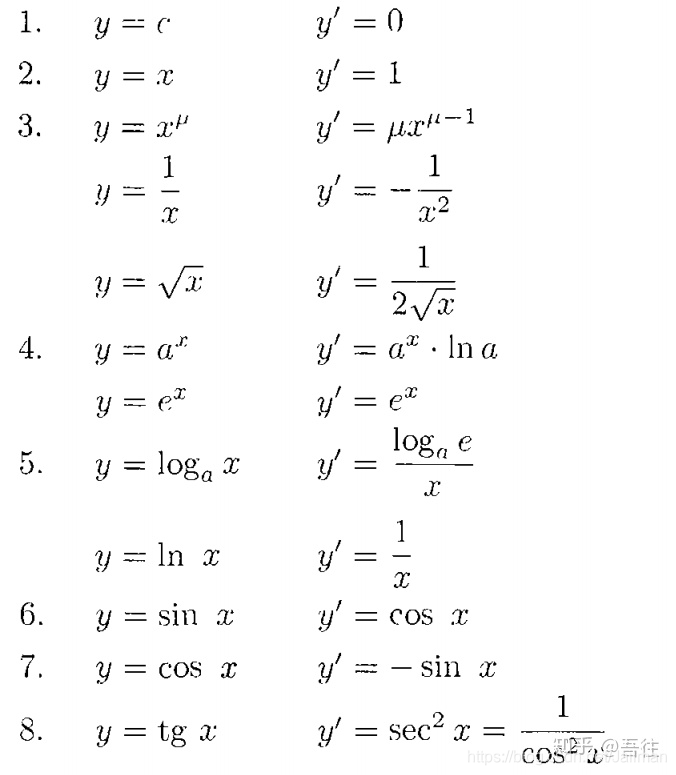
一、导数符号概述

导数符号通常由一个短撇号“'”或拉丁字母“d”来表示。在数学中，我们通常使用“f'(x)”或“df(x)/dx”来表示函数f(x)在x处的导数。这个符号不仅简洁明了，而且具有强大的数学表达力。

二、导数符号的读法与用法

1. 读法

当我们读到“f'(x)”时，我们可以读作“f关于x的导数”，或者“f的x导数”。这个读法可以帮助我们理解导数的基本含义，即函数在某一点的切线斜率或者变化率。

2. 用法

在数学公式中，导数符号常常用来表示一个函数的微分或斜率。通过使用导数符号，我们可以轻松地求出函数的极值、拐点、渐近线等重要信息。同时，在解决实际问题时，如物理学中的运动问题、经济学中的需求弹性问题等，都离不开导数的应用。

三、如何使用导数符号计算导数

求一个函数的导数并不复杂，只需掌握一定的方法和规则即可。常用的有链式法则、乘积法则、商的法则等。此外，我们还需要理解隐函数的求导方法以及偏导数的概念等。只有熟练掌握了这些基本技能，才能更好地利用导数符号进行计算。

四、总结

导数符号是数学中一个重要的概念，它不仅可以帮助我们理解函数的性质和变化规律，还可以用于解决各种实际问题。因此，我们应该认真学习和掌握导数符号的使用方法，以便更好地应用它来解决问题。同时，我们还需要注意在计算过程中保持耐心和细心，避免出现错误。只有这样，我们才能真正掌握数学的奥秘。

以上就是关于导数符号的详细解读和介绍，希望对大家有所帮助。如果想要更深入地了解导数的相关知识，建议阅读相关数学书籍或参加相关课程学习。