什么是增广矩阵
什么是增广矩阵
简介
增广矩阵(Augmented Matrix)是一个在数学领域,特别是在线性代数中经常出现的概念。增广矩阵主要应用于线性方程组的求解过程中,特别是对于消元法解线性方程组有着重要的应用。

定义与构造
增广矩阵通常由系数矩阵和常数项矩阵组合而成。对于一个线性方程组,其增广矩阵由系数矩阵在右侧拼接上该方程组的常数项矩阵形成。在增广矩阵中,左侧的系数矩阵是线性方程组的系数行排列而成的,而右侧的常数项矩阵则是由每个方程的常数项组成。

增广矩阵的用途
在解线性方程组时,增广矩阵主要用于消元法。通过对方程进行行变换(即加、减、交换行等),我们可以把系数行转换成全为0的形式,这样可以简化为更容易解的等价线性系统。由于这种处理可以合并多个线性方程组求解的步骤,所以使用增广矩阵可以提高解线性方程组的效率。
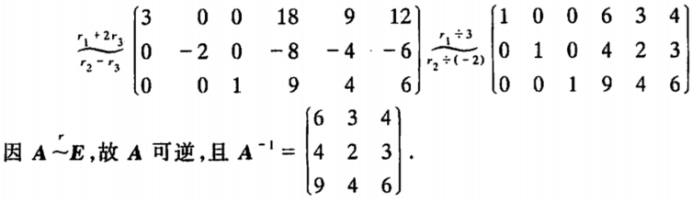
具体步骤
在运用增广矩阵解线性方程组时,我们可以遵循以下步骤:
-
构建增广矩阵:首先根据给定的线性方程组构建增广矩阵,确保每行的右侧都填上相应的常数项。
-
应用消元法:通过一系列的行变换,将增广矩阵的左侧系数行转换成全为0的形式。在这个过程中,我们通常会使用到行交换、倍数缩放和加法消元等技巧。
-
求解未知数:当增广矩阵的左侧系数行变为全为0的形式后,我们就可以直接从右侧的常数项中读取出未知数的解了。
示例
考虑以下线性方程组:
2x + 3y = 6 (第一方程)
4x - y = 5 (第二方程)对应的增广矩阵可以构建为: [a2c]3b6](c%3D5)。对上述矩阵应用消元法进行行变换后,可以得到一系列步骤以求解未知数x和y的值。此处我们不再深入描述完整的计算过程,而是指出使用增广矩阵以及相关变换来解此类问题是一种有效的手段。
总结
通过构建和使用增广矩阵,我们可以在解决复杂的线性方程组时,更为便捷地利用消元法进行求解。这种技术是线性代数中一种重要的工具,不仅有助于理解线性系统的性质,还能提高解决实际问题的效率。因此,熟练掌握增广矩阵及其相关操作是学习线性代数的重要一环。

